题目内容
【题目】如图，椭圆C： 
+ 
=1（a＞b＞0）的离心率是 
，且过点（ 
， 
）．设点A1 ， B1分别是椭圆的右顶点和上顶点，如图所示过 点A1 ， B1引椭圆C的两条弦A1E、B1F．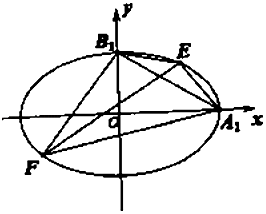
（1）求椭圆C的方程；
（2）若直线A1E与B1F的斜率是互为相反数．
①求直线EF的斜率k0②设直线EF的方程为y=k0x+b（﹣1≤b≤1）设△A1EF、△B1EF的面积分别为S1和S2 ， 求S1+S2的取值范围．
【答案】
（1）
解：由题意可知：椭圆的离心率e= 
= 
，则3a2=4c2，b2=a2﹣c2= 
a2，即a2=4b2，
将（ 
， 
）代入椭圆方程： 
，则 
，
解得：b2=1，a2=4，
椭圆C的方程 
（2）
解：①设点E（x1，y1），F（x2，y2），直线A1E，y=k（x﹣2），直线B1E：y=﹣kx+1，
则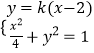 
，消去y得：（4k2+1）x2﹣16k2x+16k2﹣4=0，则2x1= 
，x1= 
，
y1=k（x1﹣2）= 
，则E（ ， ），
联立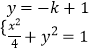 
，消去y整理得：（4k2+1）x2﹣8kx=0，x2= 
，
y2=﹣kx2+1= 
，F（ ， ），则kEF= 
= ，
②设直线EF：y= x+b，联立方程组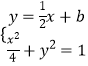 
，消去y得：x2+2bx+2b2﹣2=0，
△=（﹣2b）2﹣4（2b2﹣2）=8﹣4b2＞0，解得：﹣ 
＜b＜ ，
x1+x2=﹣2b，x1x2=2b2﹣2，丨EF丨= 
= 
，
设d1，d2分别为点A1，B1到直线EF的距离，则d1= 
，d2= 
，
则S1+S2= （d1+d2）丨EF丨=（丨b+1丨+丨b﹣1丨） 
，
∵﹣1≤b≤1时，
∴S1+S2=2 ，
由2 ∈[2，2 ]，
S1+S2∈[2，2 ]，
S1+S2的取值范围[2，2 ]
【解析】（1）由题意的离心率求得a与b关系，将（ ， ）代入椭圆方程： ，即可求得a和b的值，求得椭圆方程；（2）①将直线方程分别代入椭圆方程，利用韦达定理求得E和F点坐标，根据直线的斜率公式，即可求得直线EF的斜率k0；②将直线方程代入椭圆方程，利用韦达定理及弦长公式求得丨EF丨，利用点到直线的距离公式则A1 ， B1到直线EF的距离d1 ， d2 ， 利用三角形的面积公式及函数的单调性即可求得S1+S2的取值范围．
【考点精析】掌握椭圆的概念和椭圆的标准方程是解答本题的根本，需要知道平面内与两个定点
，
的距离之和等于常数（大于
）的点的轨迹称为椭圆,这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距；椭圆标准方程焦点在x轴：
，焦点在y轴：
．
