已知实数x.y满足约束条件$\left\{\begin{array}{l}{x-y+4≥0}\\{x+y≥0}\\{y≤4}\end{array}\right.$.则目标函数z=x-2y的最小值是-8．题目和参考答案——青夏教育精英家教网——

题目内容

20．已知实数x，y满足约束条件$\left\{\begin{array}{l}{x-y+4≥0}\\{x+y≥0}\\{y≤4}\end{array}\right.$，则目标函数z=x-2y的最小值是-8．

分析由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．

解答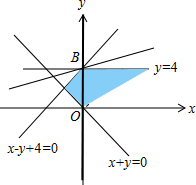解：由约束条件$\left\{\begin{array}{l}x-y+4≥0\\ x+y≥0\\ y≤4\end{array}\right.$作出可行域如图，
化目标函数z=x-2y为y=$\frac{x}{2}$-$\overline{2}$，
由图可知，当直线y=$\frac{x}{2}$-$\overline{2}$过B（0，4）时直线在y轴上的截距最大，z有最小值，等于0-2×4=-8．
故答案为：-8．

点评本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

18．定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$，函数$f（x）=|{\begin{array}{l}{2sinx}&m\\{cos2x}&{cosx}\end{array}}|$的图象关于直线x=$\frac{π}{8}$对称，则f（x）的单调递增区间为（　　）

	A．	$[kπ-\frac{3π}{8}，kπ+\frac{π}{8}]，（k∈Z）$		B．	$[kπ-\frac{π}{8}，kπ+\frac{3π}{8}]，（k∈Z）$
	C．	$[2kπ-\frac{3π}{4}，2kπ+\frac{π}{4}]，（k∈Z）$		D．	$[2kπ-\frac{π}{4}，2kπ+\frac{3π}{4}]，（k∈Z）$

19．若函数f（x）在定义域的某子区间上满足f（x）=$\frac{1}{λ}f（{x-λ}）$（λ为正实数），则称其为λ-局部倍缩函数．若函数f（x）在x∈[0，2]时，f（x）=sinπx，且x∈（2，+∞）时，f（x）为λ=2的局部倍缩函数．现有下列4个命题：
①任取x₁、x₂∈[0，+∞），都有|f（x₁）-f（x₂）|≤2恒成立；
②f（x）=2kf（x+2k）（k∈N^*），对于一切x∈[0，+∞）恒成立；③函数y=f（x）-ln（x-1）有5个零点；④对任意x＞0，若不等式f（x）≤$\frac{k}{x}$恒成立，则k的最小值是$\frac{5}{4}$．
则其中所有真命题的序号是①④．

8．已知椭圆C：$\frac{x^2}{4}+{y^2}$=1，过原点的直线与椭圆C交于A，B两点（A，B不是椭圆C的顶点）．点D在椭圆C上，且AD⊥AB，直线BD与x轴、y轴分别交于M，N两点．
（1）设直线BD，AM的斜率分别为k₁，k₂，证明存在常数λ使得k₁=λk₂，并求出λ的值；
（2）求△OMN面积的最大值．

15．下列三函数中，与sin$\frac{π}{3}$数值相同的是（　　）
①sin（nπ+$\frac{4}{3}$π）
②cos（2nπ+$\frac{π}{6}$）；
③sin（2nπ+$\frac{π}{3}$）；
④cos[（2n+1）π-$\frac{π}{6}$]；
⑤sin[（2n+1）π-$\frac{π}{3}$]（n∈Z）．

5．已知i为虚数单位，则复数$\frac{1-3i}{1+i}$=（　　）

12．已知中心在原点，焦点在坐标轴上的椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）它的离心率为$\frac{1}{2}$，一个焦点是（-1，0），过直线x=4上一点引椭圆E的两条切线，切点分别是A、B．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若在椭圆E$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的点（x₀，y₀）处的切线方程是$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1．求证：直线AB恒过定点，并求出定点的坐标；
（Ⅲ）记点C为（Ⅱ）中直线AB恒过的定点，问否存在实数λ，使得|$\overrightarrow{AC}$+|$\overrightarrow{BC}$|=λ|$\overrightarrow{AC}$|•|$\overrightarrow{BC}$|成立，若成立求出λ的值，若不存在，请说明理由．

9．在直角坐标系中，已知点F（0，1），直线l：y=-1，点H是直线l上任意一点，过点H垂直于l的直线交线段FH的中垂线于点M．记点M的轨迹为曲线Γ．
（Ⅰ）求曲线Γ的方程；
（Ⅱ）若A，B为曲线Γ上异于原点的任意两点，过A，B分别作曲线T的两条切线l₁、l₂，l₁、l₂相交于点P，且与x轴分别交于E、F，设△PEF与△OAB的面积分别为S₁、S₂．试问：是否存在实数λ使得S₁=λS₂？若存在，求出λ的值；若不存在，请说明理由．

10．sin$\frac{5π}{12}$=（　　）

$\frac{\sqrt{3}}{4}$

$\frac{\sqrt{6}-\sqrt{2}}{4}$

$\frac{\sqrt{6}+\sqrt{2}}{4}$