题目内容
设函数f(x)=loga(ax+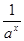 ).(1)判断函数f(x)的奇偶性;
).(1)判断函数f(x)的奇偶性;
(2)判断函数f(x)在(0,+∞)的单调性并证明.
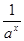 ).(1)判断函数f(x)的奇偶性;
).(1)判断函数f(x)的奇偶性;(2)判断函数f(x)在(0,+∞)的单调性并证明.
(1)由已知f(x)的定义域为R……1分,所以f(-x)=loga(a-x+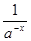 )=f(x),故f(x)为偶函数………4分.
)=f(x),故f(x)为偶函数………4分.
(2)设h(x)=ax+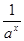 ,当a>1时,令x1>x2>0,故h(x1)>h(x2),logah(x1)>logah(x2),即f(x1)>f(x2),当a>1时,f(x)在(0,+∞)上是增函数…………10分.
,当a>1时,令x1>x2>0,故h(x1)>h(x2),logah(x1)>logah(x2),即f(x1)>f(x2),当a>1时,f(x)在(0,+∞)上是增函数…………10分.
同理可证当0<a<1时,f(x)在(0,+∞)上是减函数
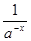 )=f(x),故f(x)为偶函数………4分.
)=f(x),故f(x)为偶函数………4分.(2)设h(x)=ax+
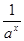 ,当a>1时,令x1>x2>0,故h(x1)>h(x2),logah(x1)>logah(x2),即f(x1)>f(x2),当a>1时,f(x)在(0,+∞)上是增函数…………10分.
,当a>1时,令x1>x2>0,故h(x1)>h(x2),logah(x1)>logah(x2),即f(x1)>f(x2),当a>1时,f(x)在(0,+∞)上是增函数…………10分.同理可证当0<a<1时,f(x)在(0,+∞)上是减函数
略

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
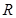 的函数
的函数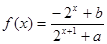 是奇函数.
是奇函数.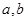 的值;
的值;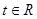 ,不等式
,不等式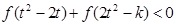 恒成立,求
恒成立,求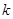 的取值范围
的取值范围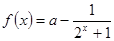 ,若
,若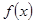 为奇函数,则
为奇函数,则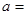 _________。
_________。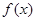 满足:对任意的
满足:对任意的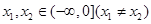 ,有
,有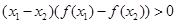 ,则当
,则当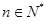 时,有
时,有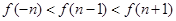
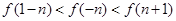

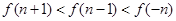
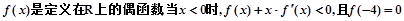 ,则不等式
,则不等式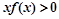 的解集为( )
的解集为( )



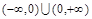 上的奇函数
上的奇函数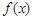 ,当
,当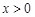 时,
时,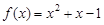 ,那么当
,那么当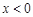 时,
时,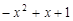
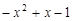
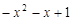
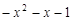
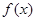 是定义在
是定义在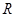 上的奇函数,当
上的奇函数,当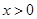 时,
时,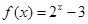 ,那么
,那么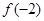 的值是( )
的值是( )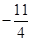
 是定义在R上的奇函数,当
是定义在R上的奇函数,当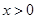 时,
时,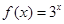 ,则
,则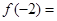 ______。
______。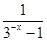 +a是奇函数,则实数a的值为 ( ).
+a是奇函数,则实数a的值为 ( ).