题目内容
已知定义域为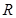 的函数
的函数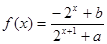 是奇函数.
是奇函数.
(1)求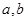 的值;
的值;
(2)若对任意的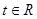 ,不等式
,不等式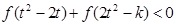 恒成立,求
恒成立,求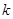 的取值范围
的取值范围
 的函数
的函数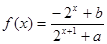 是奇函数.
是奇函数.(1)求
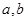 的值;
的值;(2)若对任意的
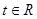 ,不等式
,不等式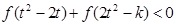 恒成立,求
恒成立,求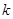 的取值范围
的取值范围解(1)因为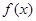 是R上的奇函数,
是R上的奇函数,
所以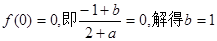 ………………………………(2分).
………………………………(2分).
从而有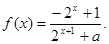
又由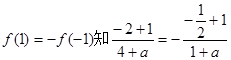 ,解得
,解得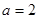 …………(6分).
…………(6分).
()由(1)知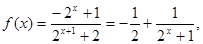
由上式易知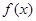 在R上为减函数,又因
在R上为减函数,又因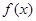 是奇函数,从而不等式(7分)
是奇函数,从而不等式(7分)
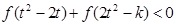
等价于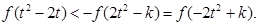 …………(9分)
…………(9分)
因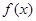 是R上的减函数,由上式推得
是R上的减函数,由上式推得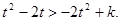 …………(10分)
…………(10分)
即对一切K*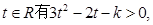 从而
从而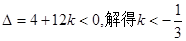
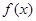 是R上的奇函数,
是R上的奇函数,所以
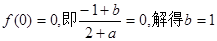 ………………………………(2分).
………………………………(2分).从而有
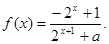
又由
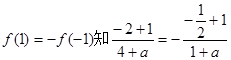 ,解得
,解得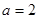 …………(6分).
…………(6分).()由(1)知
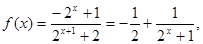
由上式易知
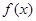 在R上为减函数,又因
在R上为减函数,又因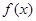 是奇函数,从而不等式(7分)
是奇函数,从而不等式(7分)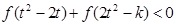
等价于
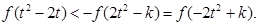 …………(9分)
…………(9分)因
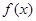 是R上的减函数,由上式推得
是R上的减函数,由上式推得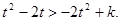 …………(10分)
…………(10分)即对一切K*
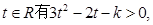 从而
从而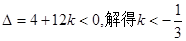
略

练习册系列答案
相关题目
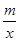 ,且f(1)=2.
,且f(1)=2.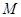 是满足下列性质的函数
是满足下列性质的函数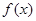 的全体, 存在非零常数
的全体, 存在非零常数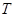 , 对任意
, 对任意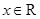 , 有
, 有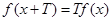 成立.
成立.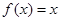 是否属于集合
是否属于集合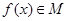 , 且
, 且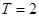 , 已知当
, 已知当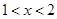 时,
时, 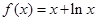 , 求当
, 求当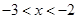 时,
时, 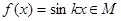 ,求实数
,求实数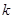 的取值范围.
的取值范围.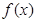 ,当
,当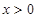 时
时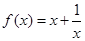 ,则
,则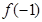 = .
= .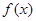 的定义域为
的定义域为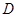 ,若存在非零实数
,若存在非零实数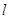 使得对于任意
使得对于任意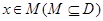 ,有
,有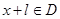 ,且f(x+l)≥f(x),则称
,且f(x+l)≥f(x),则称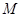 上的
上的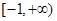 的函数
的函数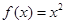 为
为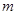 高调函数,那么实数
高调函数,那么实数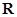 的函数
的函数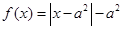 ,且
,且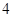 高调函数,那么实数
高调函数,那么实数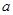 的取值范围是__________.
的取值范围是__________.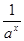 ).(1)判断函数f(x)的奇偶性;
).(1)判断函数f(x)的奇偶性;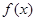 是
是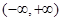 上的偶函数,若对于
上的偶函数,若对于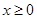 ,都有
,都有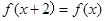
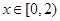 时,
时,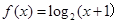 ,则
,则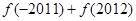 的值为( )
的值为( )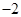
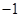
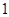
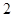
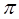 ,且当x
,且当x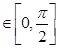 时,f(x)=sinx,则f(
时,f(x)=sinx,则f(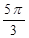 )=________。
)=________。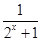 +m是奇函数,则f(-1)的值是 .
+m是奇函数,则f(-1)的值是 .