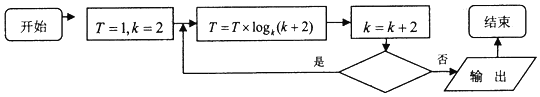题目内容
【题目】如图,在正四棱柱![]() 中,
中,![]() ,
,![]() ,建立如图所示的空间直角坐标系
,建立如图所示的空间直角坐标系![]() .
.

(1)若![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)若二面角![]() 的大小为
的大小为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)异面直线![]() 与
与![]() 所成角为
所成角为![]() ;(2)
;(2)![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ;(3)二面角
;(3)二面角![]() 的大小为
的大小为![]() ,
,![]() 的值为
的值为![]() .
.
【解析】分析:(1)由题意可得![]() 和
和![]() 的坐标,可得夹角的余弦值;
的坐标,可得夹角的余弦值;
(2)求出平面![]() 的法向量,即可求出答案;
的法向量,即可求出答案;
(3)设![]() ,表示出平面
,表示出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用二面角
的法向量,利用二面角![]() 的大小为
的大小为![]() ,即可求出t.
,即可求出t.
详解:(1)当![]() 时,
时,![]() ,,
,,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
故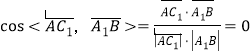 ,
,
所以异面直线![]() 与
与![]() 所成角为
所成角为![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则由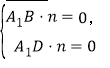 得,
得,![]()
不妨取![]() ,则
,则![]() , 此时
, 此时![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,因为
,因为![]() ,
,
则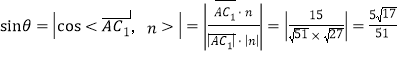 ,
,
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)由![]() 得,
得,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则由 得,
得,![]()
不妨取![]() ,则
,则![]() , 此时
, 此时![]() ,
,
又平面![]() 的法向量
的法向量![]() ,
,
故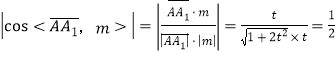 ,解得
,解得![]() ,
,
由图形得二面角![]() 大于
大于![]() ,所以符合题意.
,所以符合题意.
所以二面角![]() 的大小为
的大小为![]() ,
,![]() 的值为
的值为![]() .
.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】为了巩固全国文明城市创建成果,今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度,随机从存在违章搭建的户主中抽取了男性、女性共![]() 名进行调查,调查结果如下:
名进行调查,调查结果如下:
支持 | 反对 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
(1)根据以上数据,判断是否有![]() 的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关;
(2)现从参与调查的女户主中按此项工作的“支持”与“反对”态度用分层抽样的方法抽取![]() 人,从抽取的
人,从抽取的![]() 人中再随机地抽取
人中再随机地抽取![]() 人赠送小礼品,记这
人赠送小礼品,记这![]() 人中持“支持”态度的有
人中持“支持”态度的有![]() 人,求
人,求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
【题目】 某汽车租赁公司为了调查A, B两种车型的出租情况,现随机抽取这两种车型各50辆,分别统计了每辆车在某个星期内的出租天数,统计数据如下表:
A型车
出租天数 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 3 | 30 | 5 | 7 | 5 |
B型车
出租天数 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 10 | 10 | 15 | 10 | 5 |
(1)试根据上面的统计数据,判断这两种车型在本星期内出租天数的方差的大小关系(只需写出结果);
(2)现从出租天数为3天的汽车(仅限A, B两种车型)中随机抽取一辆,试估计这辆汽车是A型车的概率;
(3)如果两种车型每辆车每天出租获得的利润相同,该公司需要购买一辆汽车,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.
【题目】随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司做了一次抽样调查,并统计得出某款车的使用年限![]() (单位:年)与所支出的总费用
(单位:年)与所支出的总费用![]() (单位:万元)有如下的数据资料:
(单位:万元)有如下的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知![]() 对
对![]() 呈线性相关关系.
呈线性相关关系.
线性回归方程系数公式:
 ,
,![]() .
.
(1)试求线性回归方程![]() 的回归系数
的回归系数![]() ,
,![]() ;
;
(2)当使用年限为10年时,估计车的使用总费用.