题目内容
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
(1)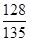 ;
;
(2)
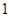
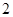

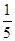
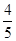
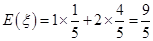 .
.
解析试题分析:(1)此题审题很重要,主要是对“每人答对其中的2题就停止答题,即闯关成功”理解,即当前两题都答正确,就可不答第三题,或第三题答对与否,不影响闯关成功,从它的对立事件考虑就显得简单,同时注意甲和乙是两个不同的常见概率模型;(2)在正确处理好(1)的前提下,此题就不难,具备知识走个程序即可.
试题解析:(1)设甲、乙闯关成功分别为 、
、 .
.
则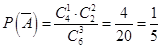 ,
,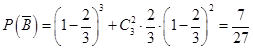 .
.
所以,甲乙至少有1人闯关成功的概率为 .
.
(2)由题意,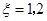 .
.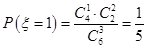 ,
,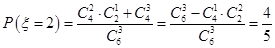
 的分布列为
的分布列为
1 2 
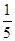
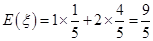 .
.
考点:概率、概率分布及数学期望

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 ,乙胜的概率为
,乙胜的概率为 ,且每局比赛胜负互不受影响.
,且每局比赛胜负互不受影响. 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为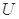 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
.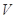 的概率;
的概率;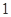 个点,连续取
个点,连续取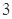 次,得到
次,得到 ,求
,求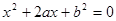 是关于
是关于 的一元二次方程.
的一元二次方程.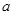 是从集合
是从集合 四个数中任取的一个数,
四个数中任取的一个数,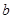 是从集合
是从集合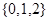 三个数中任取的一个数,求上述方程有实数根的概率;
三个数中任取的一个数,求上述方程有实数根的概率; ,
, ,求上述方程有实数根的概率.
,求上述方程有实数根的概率.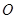 型血的人数占总人口数的比为
型血的人数占总人口数的比为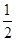 ,现从中随机抽取3人.
,现从中随机抽取3人.  ,求
,求