题目内容
一个均匀的正方体玩具,各个面上分别写有1,2,3,4,5,6,将这个玩具先后抛掷2次,求:
(1)朝上的一面数相等的概率;(2)朝上的一面数之和小于5的概率.
(1) ;(2)
;(2)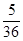
解析试题分析:每个面向上的机会均等,概率都是 ,(1)先后抛掷2次朝上的一面数相等,即相互独立事件同时发生,所求概率为
,(1)先后抛掷2次朝上的一面数相等,即相互独立事件同时发生,所求概率为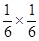 ;(2)朝上的一面数之和小于5包括
;(2)朝上的一面数之和小于5包括 ,
, 五中情况,它们是互斥关系,用互斥事件概率加法公式可求概率。
五中情况,它们是互斥关系,用互斥事件概率加法公式可求概率。
试题解析:(1)我们假定一个数字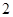 ,两次抛掷都是它,第一次是2的概率是
,两次抛掷都是它,第一次是2的概率是 ,第二次是2的概率还是
,第二次是2的概率还是 ,因为两次是且的关系,所以,两次抛掷都是2的概率是
,因为两次是且的关系,所以,两次抛掷都是2的概率是 ,也就是说朝上一面数相等的概率是
,也就是说朝上一面数相等的概率是 。
。
(2)朝上一面数之和小于5的组合有: ,而这五组的概率都是
,而这五组的概率都是 ,且是或的关系,也就是说朝上一面数之和小于5的概率是
,且是或的关系,也就是说朝上一面数之和小于5的概率是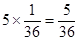
考点:(1)相互独立事件定义及概率乘法公式;(2)互斥事件定义及概率加法公式。

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次 购物量 | 1至 4件 | 5至 8件 | 9至 12件 | 13至 16件 | 17件及 以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间 (分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并估计顾客一次购物的结算时间的平均值;
(2)求一位顾客一次购物的结算时间不超过2分钟的概率.(将频率视为概率)
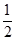 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: 的分别列与期望E
的分别列与期望E .
. ,求
,求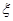 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的概率分布及数学期望.
的概率分布及数学期望.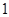 个、黄色球
个、黄色球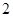 个、蓝色球
个、蓝色球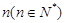 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得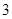 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出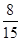 .
.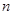 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出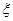 表示所摸
表示所摸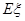 .
.