题目内容
在平面 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为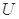 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
.
(1)定义横、纵坐标为整数的点为“整点”.在区域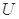 任取3个整点,求这些整点中恰有2个整点在区域
任取3个整点,求这些整点中恰有2个整点在区域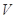 的概率;
的概率;
(2)在区域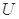 每次任取
每次任取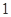 个点,连续取
个点,连续取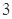 次,得到
次,得到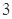 个点,记这
个点,记这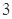 个点在区域
个点在区域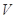 的个数为
的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(1)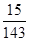
(2) 的分布列为
的分布列为

0 1 2 3 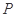
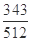
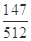
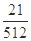
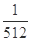
 的数学期望为
的数学期望为 .
.
解析试题分析:(1)作出平面区域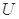 和平面区域
和平面区域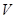 ,打出网格,找出整点,数出在区域
,打出网格,找出整点,数出在区域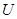 中整点的个数及这些点落在区域
中整点的个数及这些点落在区域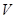 中的个数,运用排列组合知识和古典概型公式求出所求事件的概率;(2)由独立重复试验的概念知,每次在区域
中的个数,运用排列组合知识和古典概型公式求出所求事件的概率;(2)由独立重复试验的概念知,每次在区域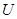 中取一点该点落在区域
中取一点该点落在区域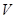 内的概率为定值,取3次,的3个点,落在区域
内的概率为定值,取3次,的3个点,落在区域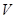 内点的个数服从二项分布,根据二项分布的概率公式和期望公式即可求出分布列与期望.
内点的个数服从二项分布,根据二项分布的概率公式和期望公式即可求出分布列与期望.
试题解析:(1)依题可知平面区域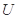 的整点为:
的整点为: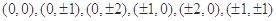 共有13个,上述整点在平面区域
共有13个,上述整点在平面区域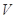 的为:
的为: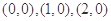 共有3个,
共有3个,
∴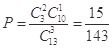 . (4分)
. (4分)
(2)依题可得,平面区域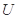 的面积为
的面积为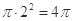 ,
,
平面区域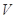 与平面区域
与平面区域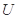 相交部分的面积为
相交部分的面积为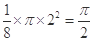 .
.
(设扇形区域中心角为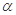 ,则
,则 得
得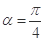 ,也可用向量的夹角公式求
,也可用向量的夹角公式求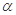 ).
).
在区域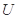 任取1个点,则该点在区域
任取1个点,则该点在区域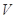 的概率为
的概率为 ,随机变量
,随机变量 的可能取值为:
的可能取值为: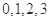 .
. ,
,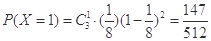 ,
, ,
,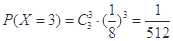 ,
,
∴ 的分布列为
的分布列为

0 1 2 3 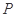
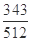
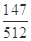
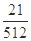
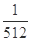
∴ 的数学期望:
的数学期望: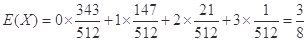 . (12分)
. (12分)
(或者: ~
~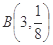 ,故
,故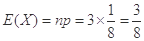 ).
).
考点:二元一次不等式组表示的平面区域,古典概型,二项分布

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
吸烟的危害很多,吸烟产生的烟雾中有近2000种有害物质,如尼古丁、氰氢酸、氨、一氧化碳、二氧化碳、吡啶、砷、铜、铅等,还有40多种致癌物,如苯并芘、朕苯胺及煤焦油等。它们随吸烟者吞咽烟雾时进入体内,对机体产生危害。为了解某市心肺疾病是否与吸烟有关,某医院随机对入院的50人进行了问卷调查,得到了如下的列联表.
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 吸烟患者 | 20 | 5 | 25 |
| 不吸烟患者 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在患心肺疾病的人群中抽3人,其中吸烟患者抽到多少人?
(2)在上述抽取的3人中选2人,求恰有一名不吸烟患者的概率;
(3)是否有99.5%的把握认为患心肺疾病与吸烟有关?
附:
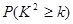 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:
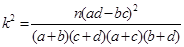 ,其中
,其中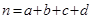
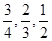 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分. .
. ,求
,求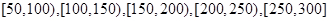 ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.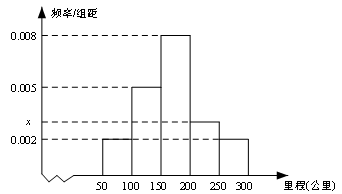
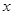 的值;
的值;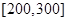 的车辆数;
的车辆数;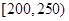 的概率.
的概率.
 ,则该学生在面试时得分的期望值为 分.
,则该学生在面试时得分的期望值为 分. 两次摸出的球颜色相同的概率是 ;
两次摸出的球颜色相同的概率是 ;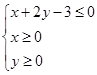 所表示的平面区域内的概率.
所表示的平面区域内的概率.