题目内容
甲乙两人进行掰手腕比赛,比赛规则规定三分钟为一局,三分钟内不分胜负为平局,当有一人赢3局就结束比赛,否则继续进行,根据以往经验,每次甲胜的概率为 ,乙胜的概率为
,乙胜的概率为 ,且每局比赛胜负互不受影响.
,且每局比赛胜负互不受影响.
(Ⅰ)求比赛4局乙胜的概率;
(Ⅱ)求在2局比赛中甲的胜局数为ξ的分布列和数学期望;
(Ⅲ)若规定赢一局得2分,平一局得1分,输一局得0分,比赛进行五局,积分有超过5分者比赛结束,否则继续进行,求甲得7分的概率.
(I)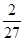 ;
;
(II) 分布列为: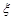
0 1 2 P 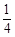
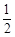
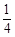
数学期望为1;
(Ⅲ)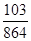
解析试题分析:(I)4局乙胜,即4局中乙3胜,且第4局为胜,前3局赛果为乙胜2局平1局或乙胜2局甲胜1局,所求概率为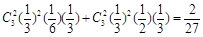 ,(II)甲的胜局数为ξ可取0,1,2,ξ取0包括输2局或平两局或1局输1局平,所以
,(II)甲的胜局数为ξ可取0,1,2,ξ取0包括输2局或平两局或1局输1局平,所以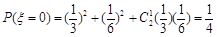 ,ξ取1包括1赢1输或1赢1平,所以
,ξ取1包括1赢1输或1赢1平,所以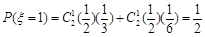 ,ξ取2包括2次都赢,所以
,ξ取2包括2次都赢,所以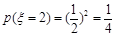 ,数学期望
,数学期望 ;(Ⅲ)甲若得7分, 要进行4局或5局比赛,且最后一局甲赢, 设比赛进行4局为事件A即为前3局要平1胜2,第4局胜,比赛进行5局为事件B即为前4局胜1平3或输1平1胜2,第5局胜,则
;(Ⅲ)甲若得7分, 要进行4局或5局比赛,且最后一局甲赢, 设比赛进行4局为事件A即为前3局要平1胜2,第4局胜,比赛进行5局为事件B即为前4局胜1平3或输1平1胜2,第5局胜,则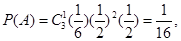
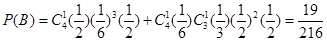 ,所以
,所以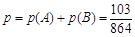 .
.
试题解析:由已知得甲赢的概率为 ,平的概率为
,平的概率为 ,输的概率为
,输的概率为 ,
,
乙赢的概率为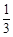 ,平的概率为
,平的概率为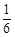 ,输的概率为
,输的概率为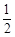 ,
,
(I)4局乙胜,即4局中乙3胜,且第4局为胜
所求的概率为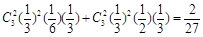
(II) 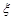 取0,1,2
取0,1,2 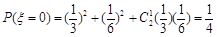
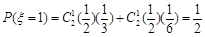
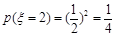
分布列如下: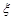
0 1 2 P 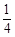
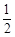
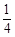

(Ⅲ)甲若得7分, 要进行4局或5局比赛,且最后一局甲赢, 设比赛进行4局事件为A,比赛进行5局事件为B,则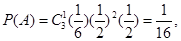
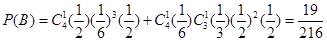 ,
,
所以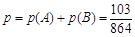
考点:概率分布列和数学期望

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 中,
中, 为
为 中点,抛物线的一部分在矩形内,点
中点,抛物线的一部分在矩形内,点 为抛物线顶点,点
为抛物线顶点,点 在抛物线上,在矩形内随机地放一点,则此点落在阴影部分的概率为 .
在抛物线上,在矩形内随机地放一点,则此点落在阴影部分的概率为 . 
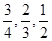 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分. .
. ,求
,求 表示事件“抽到两 题的编号分别为
表示事件“抽到两 题的编号分别为 ,且
,且 <
< ”.
”. 两次摸出的球颜色相同的概率是 ;
两次摸出的球颜色相同的概率是 ;