题目内容
设某地区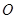 型血的人数占总人口数的比为
型血的人数占总人口数的比为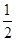 ,现从中随机抽取3人.
,现从中随机抽取3人.
(1)求3人中恰有2人为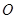 型血的概率;
型血的概率;
(2)记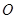 型血的人数为
型血的人数为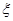 ,求
,求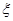 的概率分布与数学期望.
的概率分布与数学期望.
(1) ;(2)
;(2)
, 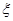
0 1 2 3 P 




解析试题分析:由已知从该地区随机抽取3人,相当于将试验独立地做了3次,并且每一次抽得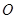 型血的人发生的概率相等均为
型血的人发生的概率相等均为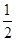 ,且各次试验之间相互独立;从而可知
,且各次试验之间相互独立;从而可知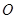 型血的人数为
型血的人数为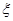 服从参数为3和
服从参数为3和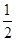 的二项分布,即
的二项分布,即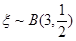 ,从而有
,从而有 (1)令k=2,则得结果;(2)由k=0,1,2,3得到
(1)令k=2,则得结果;(2)由k=0,1,2,3得到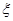 的概率分布;再由公式
的概率分布;再由公式 可求得
可求得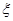 的数学期望.
的数学期望.
试题解析:(1)由题意,随机抽取一人,是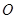 型血的概率为
型血的概率为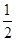 , 2分
, 2分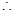 3人中有2人为
3人中有2人为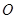 型血的概率为
型血的概率为 . 6分
. 6分
(2)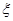 的可能取值为0,1,2,3, 8分
的可能取值为0,1,2,3, 8分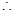
 ,
, 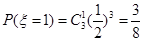 ,
, 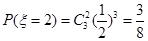 ,
,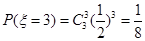 , 12分
, 12分
故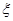 的概率分布为:
的概率分布为: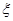
0 1 2 3 P 



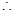
 . 14分
. 14分
考点:1.二项分布;2.数学期望.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 .
. ,求
,求 的概率分布及数学期望.
的概率分布及数学期望.
 个、黄色球
个、黄色球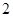 个、蓝色球
个、蓝色球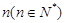 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得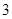 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出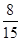 .
. 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出 表示所摸
表示所摸 .
. 表示事件“抽到两 题的编号分别为
表示事件“抽到两 题的编号分别为 ,且
,且 <
< ”.
”.
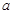 的值;
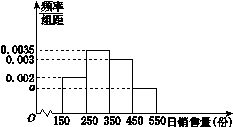
的值; (单位支),当n≥X时,求利润Y的表达式;
(单位支),当n≥X时,求利润Y的表达式;

 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求