题目内容
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,记ξ=|x-2|+|y-x|.
(1)求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率;
(2)求随机变量ξ的分布列.
(1)3,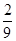 ;(2)见解析
;(2)见解析
解析试题分析:(1)通过分析x,y的取值情况,先求出|x-2|与|y-x|的最大值,从而求出ξ的最大值,分析ξ取最大值时,x,y的取值情况及x,y所有取值情况,根据古典概型公式求出所求事件的概率;(2)先分析ξ的所有可能取值及取该值时x,y的取值情况,根据古典概型公式求出分布列.
试题解析:(1)∵x,y可能的取值为1,2,3,
∴|x-2|≤1,|y-x|≤2,
∴ξ≤3,且当x=1,y=3或x=3,y=1时,ξ=3.
因此,随机变量ξ的最大值为3.(3分)
∵有放回抽两张卡片的所有情况有3×3=9种,
∴P(ξ=3)=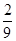 .
.
故随机变量ξ的最大值为3,事件“ξ取得最大值”的概率为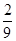 .(6分)
.(6分)
(2)ξ的所有取值为0,1,2,3.
∵ξ=0时,只有x=2,y=2这一种情况,
ξ=1时,有x=1,y=1或x=2,y=1或x=2,y=3或x=3,y=3四种情况,
ξ=2时,有x=1,y=2或x=3,y=2两种情况.
ξ=3时,有x=1,y=3或x=3,y=1两种情况.
∴P(ξ=0)= ,P(ξ=1)=
,P(ξ=1)=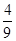 ,P(ξ=2)=
,P(ξ=2)=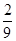 ,
,
P(ξ=3)=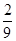 .(10分)
.(10分)
则随机变量ξ的分布列为:ξ 0 1 2 3 P 
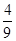
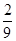
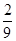
考点:古典概型,分类整合思想

练习册系列答案
相关题目
 张卡片(大小,形状都相同)上分别写有
张卡片(大小,形状都相同)上分别写有 ,
, ,
, ,
,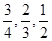 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分.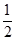 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: 的分别列与期望E
的分别列与期望E .
. ,求
,求 的概率分布及数学期望.
的概率分布及数学期望.
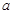 的值;
的值; (单位支),当n≥X时,求利润Y的表达式;
(单位支),当n≥X时,求利润Y的表达式;