题目内容
4.给出下列四个命题:①f(x)=sin(2x-$\frac{π}{4}$)的对称轴为x=$\frac{kπ}{2}+\frac{3π}{8}$,k∈Z;②若函数y=2cos(ax-$\frac{π}{3}$)(a>0)的最小正周期是π,则a=2;③函数f(x)=sinxcosx-1的最小值为-$\frac{3}{2}$;④函数y=sin(x+$\frac{π}{4}$)在[-$\frac{π}{2},\frac{π}{2}$]上是增函数,其中正确命题的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 求出函数的对称轴方程判断①;由周期公式求出a值判断②;利用倍角公式化简,进一步求出函数的最小值判断③;由函数的单调性判断④.
解答 解:①由$2x-\frac{π}{4}=kπ+\frac{π}{2}$,得x=$\frac{kπ}{2}+\frac{3π}{8}$,k∈Z,
∴f(x)=sin(2x-$\frac{π}{4}$)的对称轴为x=$\frac{kπ}{2}+\frac{3π}{8}$,k∈Z,①正确;
②若函数y=2cos(ax-$\frac{π}{3}$)(a>0)的最小正周期是π,则$\frac{2π}{a}=π$,即a=2,②正确;
③函数f(x)=sinxcosx-1=$\frac{1}{2}sin2x-1$,最小值为-$\frac{3}{2}$,③正确;
④当x∈[-$\frac{π}{2},\frac{π}{2}$]时,x$+\frac{π}{4}∈$[-$\frac{π}{4},\frac{3π}{4}$],∴函数y=sin(x+$\frac{π}{4}$)在[-$\frac{π}{2},\frac{π}{2}$]上不是单调函数,④错误.
∴正确命题的个数是3个.
故选:C.
点评 本题考查命题的真假判断与应用,考查了三角函数的图象和性质,是基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
14.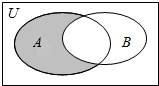 设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )
设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )
 设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )
设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )| A. | {1,2,5,6} | B. | {1} | C. | {2} | D. | {1,2,3,4} |
15.已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+1的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | $[-\frac{5}{4},+∞)$ | B. | [1,2] | C. | $[-\frac{5}{4},1]$ | D. | [-1,1] |
12.袋中有10个外形相同的球,其中5个白球,3个黑球,2个红球,从中任意取出一球,已知它不是白球,则它是黑球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
9.焦点分别为(-2,0),(2,0)且经过点(2,3)的双曲线的标准方程为( )
| A. | x2-$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}-{y}^{2}=1$ | C. | y2-$\frac{{x}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}=1$ |
16.下列各组函数中,表示同一函数的是( )
| A. | $y=x+1与y=\frac{{{x^2}+x}}{x}$ | B. | $f(x)=\frac{x^2}{{{{({\sqrt{x}})}^2}}}与g(x)=x$ | ||
| C. | $f(x)=x\frac{|x|}{x}与f(t)=\left\{\begin{array}{l}t(t>0)\\-t(t<0)\end{array}\right.$ | D. | $f(x)=|x|与g(x)=\left\{\begin{array}{l}x(x>0)\\-x(x<0)\end{array}\right.$ |
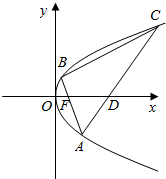 已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.
已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.