题目内容
5.已知函数f(x)=log2(x-$\frac{1}{x}$),x∈[a,+∞)的值域为[0,+∞),则实数a的值为$\frac{\sqrt{5}+1}{2}$.分析 由已知中函数的定义域可得a>0,结合对数函数的单调性和复合函数的单调性,分析函数为增函数后,可得当x=a时,a-$\frac{1}{a}$=1,解得答案.
解答 解:∵函数f(x)=log2(x-$\frac{1}{x}$),x∈[a,+∞),
则a>0,
由y=log2x在定义域上为增函数,y=x-$\frac{1}{x}$在[a,+∞)上为增函数,
故函数f(x)=log2(x-$\frac{1}{x}$)在[a,+∞)上为增函数,
若函数f(x)=log2(x-$\frac{1}{x}$),x∈[a,+∞)的值域为[0,+∞),
故当x=a时,a-$\frac{1}{a}$=1,
解得:a=$\frac{\sqrt{5}+1}{2}$,或a=$\frac{-\sqrt{5}+1}{2}$(舍去)
故实数a的值为$\frac{\sqrt{5}+1}{2}$.
故答案为:$\frac{\sqrt{5}+1}{2}$
点评 本题考查的知识点是对数函数的图象和性质,复合函数的单调性,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
15.在△ABC中,(sinA+sinB)(sinA-sinB)≤sinC(sinC-sinB),则A的取值范围是( )
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6},π$) | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3},π$) |
13.计算22+42+62+…+1002的算法的程序框图是( )
| A. | 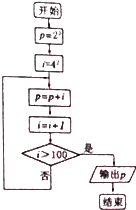 | B. | 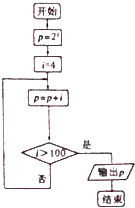 | C. | 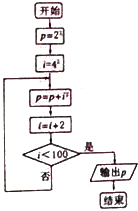 | D. | 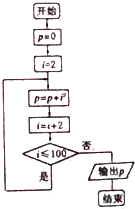 |