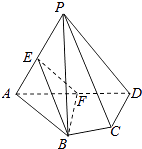
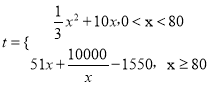ЬтФПФкШн
ЁОЬтФПЁПвбжЊЪ§Са{an}ЕФИїЯюОљЮЊе§Ъ§ЃЌЦфЧАnЯюЕФКЭЮЊSnЃЌЧвЖдШЮвтЕФmЃЌnЁЪN*ЃЌ
ЖМга(SmЃЋnЃЋS1)2ЃН4a2ma2nЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓжЄЃК{an}ЮЊЕШБШЪ§СаЃЛ
ЃЈ3ЃЉвбжЊЪ§Са{cn}ЃЌ{dn}Тњзу|cn|ЃН|dn|ЃНanЃЌp(pЁн3)ЪЧИјЖЈЕФе§ећЪ§ЃЌЪ§Са{cn}ЃЌ{dn}ЕФЧАpЯюЕФКЭЗжБ№ЮЊTpЃЌRpЃЌЧвTpЃНRpЃЌЧѓжЄЃКЖдШЮвте§ећЪ§k(1ЁмkЁмp)ЃЌckЃНdkЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉБОЬтВЩгУИГжЕЗЈЃЌдквбжЊЕШЪНжаСю![]() ЕУЕУГі
ЕУЕУГі![]() ЕФЙиЯЕЃЛЃЈ2ЃЉвВВЩгУИГжЕЗЈЃЌБОЬтФбЕудкгквбжЊЬѕМўжаЕФЦНЗНЕФДІРэЃЌЮЊДЫЯШШЁ
ЕФЙиЯЕЃЛЃЈ2ЃЉвВВЩгУИГжЕЗЈЃЌБОЬтФбЕудкгквбжЊЬѕМўжаЕФЦНЗНЕФДІРэЃЌЮЊДЫЯШШЁ![]() КЭ
КЭ![]() ЃЌЫљЕУСНСЊСЂНсКЯЃЈ1ЃЉПЩЕУ
ЃЌЫљЕУСНСЊСЂНсКЯЃЈ1ЃЉПЩЕУ![]() ЃЌШЛКѓСю
ЃЌШЛКѓСю![]() ЕУ
ЕУ![]() ЃЌСю
ЃЌСю![]() ЕУ
ЕУ![]() ЃЌДЫСНЪНЯрГ§ЕУ
ЃЌДЫСНЪНЯрГ§ЕУ ЃЌвђДЫ
ЃЌвђДЫ ЃЌМД
ЃЌМД![]() ЃЌЯТУцДІРэЗНЗЈДѓМвгІИУКмЧхГўСЫЃЌгЩДЫЪНга
ЃЌЯТУцДІРэЗНЗЈДѓМвгІИУКмЧхГўСЫЃЌгЩДЫЪНга![]() ЃЌЯргІСНЪНЯрМѕПЩжЄЕУНсТлЃЛЃЈ3ЃЉгУЗДжЄЗЈжЄУїЃЌгЩЃЈ1ЃЉ
ЃЌЯргІСНЪНЯрМѕПЩжЄЕУНсТлЃЛЃЈ3ЃЉгУЗДжЄЗЈжЄУїЃЌгЩЃЈ1ЃЉ![]() ЃЌШє
ЃЌШє![]() ЃЌВЛЗСЩш
ЃЌВЛЗСЩш![]() ЃЌ
ЃЌ ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ ![]() ЃЌетгывбжЊTpЃНRpУЌЖмЃЌДгЖј
ЃЌетгывбжЊTpЃНRpУЌЖмЃЌДгЖј![]() ЃЌгкЪЧ
ЃЌгкЪЧ![]() ЃЌдђ
ЃЌдђ![]() ЃЌвРДЮПЩжЄУїЬтЩшНсТл.
ЃЌвРДЮПЩжЄУїЬтЩшНсТл.
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩ(SmЃЋnЃЋS1)2ЃН4a2na2mЃЌЕУ(S2ЃЋS1)2ЃН4aЃЌМД(a2ЃЋ2a1)2ЃН4aЃЎ
вђЮЊa1ЃО0ЃЌa2ЃО0ЃЌЫљвдa2ЃЋ2a1ЃНa2ЃЌМДЃН2ЃЎ 3Зж
жЄУїЃКЃЈ2ЃЉЃЈЗНЗЈвЛЃЉСюmЃН1ЃЌnЃН2ЃЌЕУ(S3ЃЋS1)2ЃН4a2a4ЃЌМД(2a1ЃЋa2ЃЋa3)2ЃН4a2a4ЃЌ
СюmЃНnЃН2ЃЌЕУS4ЃЋS1ЃН2a4ЃЌМД2a1ЃЋa2ЃЋa3ЃНa4ЃЎ
Ыљвдa4ЃН4a2ЃН8a1ЃЎ
гжвђЮЊЃН2ЃЌЫљвдa3ЃН4a1ЃЎ 6Зж
гЩ(SmЃЋnЃЋS1)2ЃН4a2na2mЃЌЕУ(SnЃЋ1ЃЋS1)2ЃН4a2na2ЃЌ(SnЃЋ2ЃЋS1)2ЃН4a2na4ЃЎ
СНЪНЯрГ§ЃЌЕУЃНЃЌЫљвдЃНЃН2ЃЎ
МДSnЃЋ2ЃЋS1ЃН2(SnЃЋ1ЃЋS1)ЃЌ
ДгЖјSnЃЋ3ЃЋS1ЃН2(SnЃЋ2ЃЋS1)ЃЎ
ЫљвдanЃЋ3ЃН2anЃЋ2ЃЌЙЪЕБnЁн3ЪБЃЌ{an}ЪЧЙЋБШЮЊ2ЕФЕШБШЪ§СаЃЎ
гжвђЮЊa3ЃН2a2ЃН4a1ЃЌДгЖјanЃНa1ЁЄ2 nЃ1ЃЌnЁЪN*ЃЎ
ЯдШЛЃЌanЃНa1ЁЄ2 nЃ1ТњзуЬтЩшЃЌ
вђДЫ{an}ЪЧЪзЯюЮЊa1ЃЌЙЋБШЮЊ2ЕФЕШБШЪ§СаЃЎ 10Зж
ЃЈЗНЗЈЖўЃЉдк(SmЃЋnЃЋS1)2ЃН4a2na2mжаЃЌ
СюmЃНnЃЌЕУS2nЃЋS1ЃН2a2nЃЎ Ђй
СюmЃНnЃЋ1ЃЌЕУS2nЃЋ1ЃЋS1ЃН2ЃЌ Ђк
дкЂйжаЃЌгУnЃЋ1ДњnЕУЃЌS2nЃЋ2ЃЋS1ЃН2a2nЃЋ2ЃЎ Ђл
ЂкЃЂйЃЌЕУa2nЃЋ1ЃН2Ѓ2a2nЃН2(Ѓ)ЃЌ Ђм
ЂлЃЂкЃЌЕУa2nЃЋ2ЃН2a2nЃЋ2Ѓ2ЃН2(Ѓ)ЃЌ Ђн
гЩЂмЂнЕУa2nЃЋ1ЃНЃЎ Ђо 8Зж
ЂоДњШыЂмЃЌЕУa2nЃЋ1ЃН2a2nЃЛЂоДњШыЂнЕУa2nЃЋ2ЃН2a2nЃЋ1ЃЌ
ЫљвдЃНЃН2ЃЎгжЃН2ЃЌ
ДгЖјanЃНa1ЁЄ2 nЃ1ЃЌnЁЪN*ЃЎ
ЯдШЛЃЌanЃНa1ЁЄ2 nЃ1ТњзуЬтЩшЃЌ
вђДЫ{an}ЪЧЪзЯюЮЊa1ЃЌЙЋБШЮЊ2ЕФЕШБШЪ§СаЃЎ 10Зж
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌanЃНa1ЁЄ2 nЃ1ЃЎ
вђЮЊ|cp|ЃН|dp|ЃНa1ЁЄ2pЃ1ЃЌЫљвдcpЃНdpЛђcpЃНЃdpЃЎ
ШєcpЃНЃdpЃЌВЛЗСЩшcpЃО0ЃЌdpЃМ0ЃЌ
дђTpЁнa1ЁЄ2pЃ1Ѓ(a1ЁЄ2pЃ2ЃЋa1ЁЄ2pЃ3ЃЋ ЃЋa1)ЃНa1ЁЄ2pЃ1Ѓa1ЁЄ(2pЃ1Ѓ1)ЃНa1ЃО0ЃЎ
RpЁмЃa1ЁЄ2pЃ1ЃЋ(a1ЁЄ2pЃ2ЃЋa1ЁЄ2pЃ3ЃЋ ЃЋa1)ЃНЃa1ЁЄ2pЃ1ЃЋa1ЁЄ(2pЃ1Ѓ1)ЃНЃa1ЃМ0ЃЎ
етгыTpЃНRpУЌЖмЃЌЫљвдcpЃНdpЃЎ
ДгЖјTpЃ1ЃНRpЃ1ЃЎ
гЩЩЯжЄУїЃЌЭЌРэПЩЕУcpЃ1ЃНdpЃ1ЃЎШчДЫЯТШЅЃЌПЩЕУcpЃ2ЃНdpЃ2ЃЌcpЃ3ЃНdpЃ3ЃЎЃЌc1ЃНd1ЃЎ
МДЖдШЮвте§ећЪ§k(1ЁмkЁмp)ЃЌckЃНdkЃЎ 16Зж

ЁОЬтФПЁППеЦјжЪСПжївЊЪмЮлШОЮяХХЗХСПМАДѓЦјРЉЩЂЕШвђЫиЕФгАЯьЃЌФГЪаЛЗБЃМрВтеО2014Фъ10дТСЌај10ЬьЃЈДгзѓЕНгвЖдгІ1КХжС10КХЃЉВЩМЏИУЪаФГЕиЦНОљЗчЫйМАПеЦјжабѕЛЏЮяЕФШеОљХЈЖШЪ§ОнЃЌжЦГЩЩЂЕуЭМШчЭМЫљЪОЃЎ
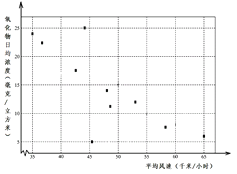
ЃЈЂёЃЉЭЌбЇМзДгет10ЬьжаЫцЛњГщШЁСЌај5ЬьЕФвЛзщЪ§ОнЃЌМЦЫуЛиЙщжБЯпЗНГЬЃЎЪдЧѓСЌај5ЬьЕФвЛзщЪ§ОнжаЧЁКУЭЌЪБАќКЌбѕЛЏЮяШеОљХЈЖШзюДѓгызюаЁжЕЕФИХТЪЃЛ
ЃЈЂђЃЉЯжга30УћбЇЩњЃЌУПШЫШЮШЁ5ЬьЪ§ОнЃЌЖдгІМЦЫуГі30ИіВЛЭЌЕФЛиЙщжБЯпЗНГЬЃЎвбжЊ30зщЪ§ОнжагаАќКЌбѕЛЏЮяШеОљХЈЖШзюжЕЕФга14зщЃЎЯжВЩгУет30ИіЛиЙщЗНГЬЖдФГвЛЬьЦНОљЗчЫйЯТЕФбѕЛЏЮяШеОљХЈЖШНјаадЄВтЃЌШєдЄВтжЕгыЪЕВтжЕВюЕФОјЖджЕаЁгк2ЃЌдђГЦжЎЮЊЁАФтКЯаЇЙћКУЁБЃЌЗёдђЮЊЁАФтКЯаЇЙћВЛКУЁБЃЎИљОнвдЩЯаХЯЂЭъГЩЯТСа2ЁС2СЊБэЃЌВЂЗжЮіЪЧЗёга95%вдЩЯЕФАбЮеЫЕФтКЯаЇЙћгыбЁШЁЪ§ОнЪЧЗёАќКЌбѕЛЏЮяШеОљХЈЖШзюжЕгаЙиЃЎ
дЄВтаЇЙћКУ | ФтКЯаЇЙћВЛКУ | КЯМЦ | |
Ъ§ОнгаАќКЌзюжЕ | 5 | ||
Ъ§ОнЮоАќКЌзюжЕ | 4 | ||
КЯМЦ |
ВЮПМЪ§ОнЃК
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
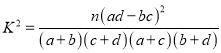 ЃЈЦфжа
ЃЈЦфжа![]() ЃЉ.
ЃЉ.