题目内容
11．解不等式：-1＜$\frac{-2λ+10}{\sqrt{{λ}^{2}+4}•\sqrt{29}}$＜0．分析 从代数式的形式发现所求实质是向量$\overrightarrow{a}$=（-2，5），$\overrightarrow{b}$=（λ，2）的夹角范围，由数量积公式解答．
解答 解：因为$\frac{-2λ+10}{\sqrt{{λ}^{2}+4}•\sqrt{29}}$是向量$\overrightarrow{a}$=（-2，5），$\overrightarrow{b}$=（λ，2）的夹角的余弦值，
所以不等式：-1＜$\frac{-2λ+10}{\sqrt{{λ}^{2}+4}•\sqrt{29}}$＜0说明两个向量的夹角大于90°，所以不等式的解集为（5，+∞）．
点评 本题考查了向量数量积公式的运用；关键是从代数式的形式发现问题的实质解之．
练习册系列答案
相关题目
1．双曲线$\frac{x^2}{13}-\frac{y^2}{3}=1$的渐近线与圆（x-4）2+y2=r2（r＞0）相切，则r=（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | $\sqrt{3}$ |
2．如图所示程序框图，则满足|x|+|y|≤2的输出的有序实数对（x，y）的概率为（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{3}{32}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
16．已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是（ ）
| A． | 若α，β垂直于同一平面，则α与β平行 | |
| B． | 若m，n平行于同一平面，则m与n平行 | |
| C． | 若α，β不平行，则在α内不存在与β平行的直线 | |
| D． | 若m，n不平行，则m与n不可能垂直于同一平面 |
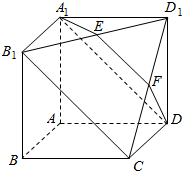如图所示，在多面体A1B1D1DCBA中，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1的中点，过A1，D，E的平面交CD1于F．
如图，AB为圆O的直径，E为AB 的延长线上一点，过E作圆O的切线，切点为C，过A作直线EC的垂线，垂足为D．若AB=4．CE=2$\sqrt{3}$，则 AD=3．