题目内容
3.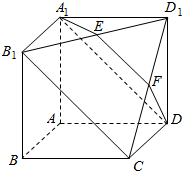 如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.
如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.(Ⅰ)证明:EF∥B1C;
(Ⅱ)求二面角E-A1D-B1的余弦值.
分析 (Ⅰ)通过四边形A1B1CD为平行四边形,可得B1C∥A1D,利用线面平行的判定定理即得结论;
(Ⅱ)以A为坐标原点,以AB、AD、AA1所在直线分别为x、y、z轴建立空间直角坐标系A-xyz,设边长为2,则所求值即为平面A1B1CD的一个法向量与平面A1EFD的一个法向量的夹角的余弦值的绝对值,计算即可.
解答 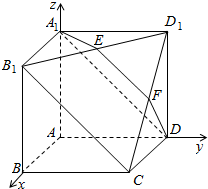 (Ⅰ)证明:∵B1C=A1D且A1B1=CD,
(Ⅰ)证明:∵B1C=A1D且A1B1=CD,
∴四边形A1B1CD为平行四边形,
∴B1C∥A1D,
又∵B1C?平面A1EFD,
∴B1C∥平面A1EFD,
又∵平面A1EFD∩平面B1CD1=EF,
∴EF∥B1C;
(Ⅱ)解:以A为坐标原点,以AB、AD、AA1所在直线分别为x、y、z轴建立空间直角坐标系A-xyz如图,设边长为2,
∵AD1⊥平面A1B1CD,∴$\overrightarrow{A{D}_{1}}$=(0,2,2)为平面A1B1CD的一个法向量,
设平面A1EFD的一个法向量为$\overrightarrow{n}$=(x,y,z),
又∵$\overrightarrow{{A}_{1}D}$=(0,2,-2),$\overrightarrow{{A}_{1}E}$=(1,1,0),
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}D}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}E}=0}\end{array}\right.$,$\left\{\begin{array}{l}{2y-2z=0}\\{x+y=0}\end{array}\right.$,
取y=1,得$\overrightarrow{n}$=(-1,1,1),
∴cos<$\overrightarrow{n}$,$\overrightarrow{A{D}_{1}}$>=$\frac{\overrightarrow{A{D}_{1}}•\overrightarrow{n}}{|\overrightarrow{A{D}_{1}}||\overrightarrow{n}|}$=$\frac{\sqrt{6}}{3}$,
∴二面角E-A1D-B1的余弦值为$\frac{\sqrt{6}}{3}$.
点评 本题考查空间中线线平行的判定,求二面角的三角函数值,注意解题方法的积累,属于中档题.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案甲养猪场猪重频数分布表
| 猪的重量分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 8 | 20 | 42 | 22 | 8 |
| 猪的重量分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 4 | 12 | 42 | 32 | 10 |
(Ⅱ)已知乙养猪场出栏一头猪的利润y(单位:百元)与其重量x(单位:公斤)的关系为:y=$\left\{\begin{array}{l}{-2(x<94)}\\{2(94≤x<102)}\\{4(x≥102)}\end{array}\right.$估计乙养猪场平均每出栏一头猪的利润.
| A. | |$\overrightarrow{b}$|=1 | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$•$\overrightarrow{b}$=1 | D. | (4$\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{BC}$ |
| A. | (-∞,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,+∞) |
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1上的动点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1上的动点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.