题目内容
1. 如图,AB为圆O的直径,E为AB 的延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4.CE=2$\sqrt{3}$,则 AD=3.
如图,AB为圆O的直径,E为AB 的延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4.CE=2$\sqrt{3}$,则 AD=3.
分析 连接OC,则OC⊥DE,可得$\frac{OC}{AD}=\frac{OE}{AE}$,由切割线定理可得CE2=BE•AE,求出BE,即可得出结论.
解答 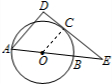 解:连接OC,则OC⊥DE,
解:连接OC,则OC⊥DE,
∵AD⊥DE,
∴AD∥OC,
∴$\frac{OC}{AD}=\frac{OE}{AE}$
由切割线定理可得CE2=BE•AE,
∴12=BE•(BE+4),
∴BE=2,
∴OE=4,
∴$\frac{2}{AD}=\frac{4}{6}$,
∴AD=3
故答案为:3.
点评 本题考查切割线定理,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设a、b都是不等于1的正数,则“3a>3b>3”是“loga3<logb3”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
9.设α,β是两个不同的平面,m是直线且m?α,“m∥β“是“α∥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.下列函数中,既不是奇函数,也不是偶函数的是( )
| A. | y=x+sin2x | B. | y=x2-cosx | C. | y=2x+$\frac{1}{{2}^{x}}$ | D. | y=x2+sinx |
6.设$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,“$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|”是“$\overrightarrow{a}$$∥\overrightarrow{b}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.设x∈R,则“x>1“是“x3>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.下列双曲线中,渐近线方程为y=±2x的是( )
| A. | x2-$\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}$-y2=1 | C. | x2-$\frac{y^2}{2}$=1 | D. | $\frac{x^2}{2}$-y2=1 |