题目内容
已知函数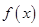 定义在
定义在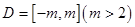 上且
上且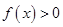 ,对于任意实数
,对于任意实数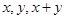
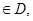 都有
都有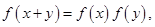 且
且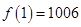 ,设函数
,设函数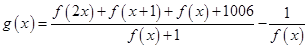 的最大值和最小值分别为
的最大值和最小值分别为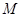 和
和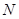 ,则
,则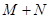 = .
= .
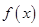 定义在
定义在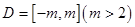 上且
上且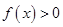 ,对于任意实数
,对于任意实数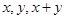
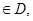 都有
都有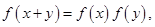 且
且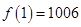 ,设函数
,设函数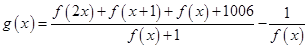 的最大值和最小值分别为
的最大值和最小值分别为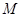 和
和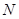 ,则
,则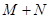 = .
= .
试题分析:由题意,
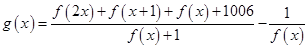
=
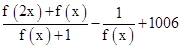 =f(x)-
=f(x)-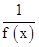 +1006
+1006∵h(x)=f(x)-
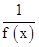 ,∴h(-x)=-h(x),即函数h(x)是奇函数
,∴h(-x)=-h(x),即函数h(x)是奇函数而
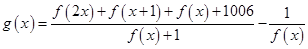 的最大值和最小值分别为M和N,
的最大值和最小值分别为M和N,∴M+N=2012,故答案为2012.
点评:中档题,关键是理解题意,将“复杂的”函数关系,化简为f(x)-
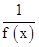 +1006。
+1006。
练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
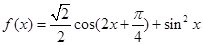
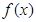 的最小正周期;
的最小正周期;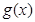 对任意
对任意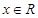 ,有
,有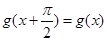 ,且当
,且当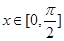 时,
时,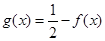 ;求函数
;求函数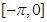 上的解析式。
上的解析式。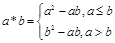 ,设
,设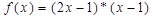 ,且关于x的方程
,且关于x的方程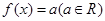 恰有三个互不相等的实数根,则实数
恰有三个互不相等的实数根,则实数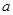 的取值范围是
的取值范围是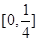
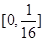
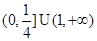
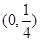
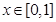 ,总有
,总有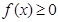 ;②
;②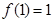 ;③若
;③若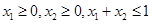 ,则有
,则有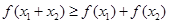 成立.
成立. 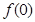 的值;(2) 函数
的值;(2) 函数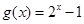 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明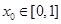 ,使得
,使得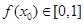 ,且
,且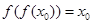 ,求证:
,求证:
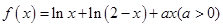 。
。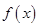 的单调区间。
的单调区间。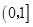 上的最大值为
上的最大值为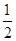 ,求a的值。
,求a的值。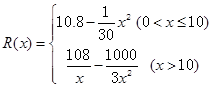
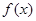 是定义在
是定义在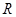 上的奇函数,且当
上的奇函数,且当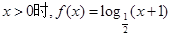 ,设
,设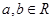 ,给出三个条件:①
,给出三个条件:①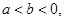 ②
② ,③
,③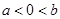 .其中可以推出
.其中可以推出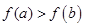 的条件共有 个.
的条件共有 个.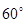 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为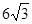 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段 与两腰长的和)要最小.
与两腰长的和)要最小.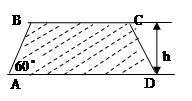
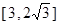 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?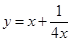 (
(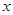 >0)取最小值时相应的
>0)取最小值时相应的