题目内容
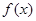 是定义在
是定义在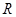 上的奇函数,且当
上的奇函数,且当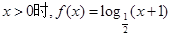 ,设
,设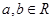 ,给出三个条件:①
,给出三个条件:①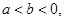 ②
② ,③
,③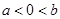 .其中可以推出
.其中可以推出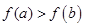 的条件共有 个.
的条件共有 个.3
试题分析:∵
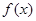 是定义在
是定义在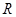 上的奇函数,且当
上的奇函数,且当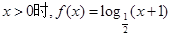 ,当
,当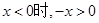
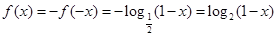 ,∴当x>0时,函数f(x)单调递减,
,∴当x>0时,函数f(x)单调递减,当x<0时,函数f(x)单调递减,故由
 得
得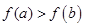 ,由
,由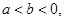 得f(a)>f(b),由
得f(a)>f(b),由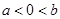 得
得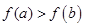 ,故可以推出
,故可以推出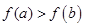 的条件共有3个。
的条件共有3个。点评:利用函数的单调性比较大小是解决此类问题的常用方法,解题时需注意运用

练习册系列答案
相关题目
题目内容
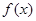 是定义在
是定义在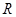 上的奇函数,且当
上的奇函数,且当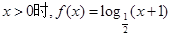 ,设
,设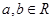 ,给出三个条件:①
,给出三个条件:①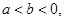 ②
② ,③
,③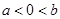 .其中可以推出
.其中可以推出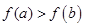 的条件共有 个.
的条件共有 个.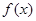 是定义在
是定义在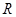 上的奇函数,且当
上的奇函数,且当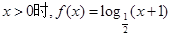 ,当
,当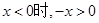
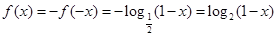 ,∴当x>0时,函数f(x)单调递减,
,∴当x>0时,函数f(x)单调递减, 得
得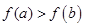 ,由
,由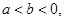 得f(a)>f(b),由
得f(a)>f(b),由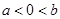 得
得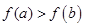 ,故可以推出
,故可以推出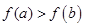 的条件共有3个。
的条件共有3个。