题目内容
17.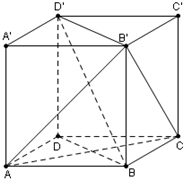 正方体ABCD-A′B′C′D′中,求证:
正方体ABCD-A′B′C′D′中,求证:(1)AC⊥平面B′D′DB;
(2)BD与B′C的夹角的余弦值.
分析 (1)证明AC⊥BD,AC⊥BB′,通过直线与平面垂直的判定定理即可证明.
(2)由BD∥B′D′,可得∠CB′D′即为BD与B′C的夹角,设正方体的边长为1,则可求B′D′=B′C=CD′=$\sqrt{2}$,即∠CB′D′=60°,从而可求BD与B′C的夹角的余弦值.
解答 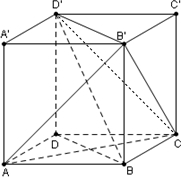 证明:(1)正方体ABCD-A′B′C′D′,B′B⊥平面ABCD,AC?平面ABCD,
证明:(1)正方体ABCD-A′B′C′D′,B′B⊥平面ABCD,AC?平面ABCD,
∴AC⊥BB′,
又∵AC、BD是正方形的对角线,∴AC⊥BD,又BD∩B′B=B,
∴AC⊥平面BB′D′D;
(2)∵BD∥B′D′,
∴可得∠CB′D′即为BD与B′C的夹角,
设正方体的边长为1,则可求:B′D′=B′C=CD′=$\sqrt{2}$,即△B′CD′为等边三角形.
∴∠CB′D′=60°,
∴cos∠CB′D′=$\frac{1}{2}$,即BD与B′C的夹角的余弦值为$\frac{1}{2}$.
点评 本题主要考查了直线与平面垂直的判定,异面直线及其所成的角,考查了空间想象能力和推论论证能力,属于基本知识的考查.

练习册系列答案
相关题目
7.天文学家经研究认为:“地球和火星在太阳系中各方面比较接近,而地球有生命,进而认为火星上也有生命存在”,这是什么推理( )
| A. | 归纳推理 | B. | 类比推理 | C. | 演绎推理 | D. | 反证法 |
7.数列{an}中,已知a1=1,a2=2,an+2=an+1-an(n∈N*),则a2015=( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
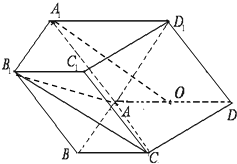 如图,在四棱柱ABCD-A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点. 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5、8.
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为5、8.