题目内容
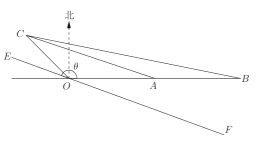
【题目】如图,![]() 为信号源点,
为信号源点,![]() 、
、![]() 、
、![]() 是三个居民区,已知
是三个居民区,已知![]() 、
、![]() 都在
都在![]() 的正东方向上,
的正东方向上,![]() ,
,![]() ,
,![]() 在
在![]() 的北偏西45°方向上,
的北偏西45°方向上,![]() ,现要经过点
,现要经过点![]() 铺设一条总光缆直线
铺设一条总光缆直线![]() (
(![]() 在直线
在直线![]() 的上方),并从
的上方),并从![]() 、
、![]() 、
、![]() 分别铺设三条最短分支光缆连接到总光缆
分别铺设三条最短分支光缆连接到总光缆![]() ,假设铺设每条分支光缆的费用与其长度的平方成正比,比例系数为1元/
,假设铺设每条分支光缆的费用与其长度的平方成正比,比例系数为1元/![]() ,设
,设![]() ,(
,(![]() ),铺设三条分支光缆的总费用为
),铺设三条分支光缆的总费用为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
【答案】(1)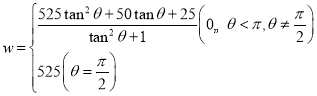 ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)对直线![]() 的斜率是否存在分类讨论,求出
的斜率是否存在分类讨论,求出![]() 三点到直线
三点到直线![]() 的距离,铺设三条分光缆的总费用即可求
的距离,铺设三条分光缆的总费用即可求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)由(1)中的表达式利用换元法,利用基本不等式,可求![]() 的最小值及此时
的最小值及此时![]() 的值.
的值.
(1) 以点![]() 位坐标原点,
位坐标原点,![]() 为
为![]() 轴建立直角坐标系,
轴建立直角坐标系,
则![]() ,
,
当直线![]() 的斜率不存在,即
的斜率不存在,即![]() 时,
时,
![]() 三点到直线
三点到直线![]() 的距离分别为10,20,5
的距离分别为10,20,5
所以此时![]() =
=![]() ,
,
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,
![]() 三点到直线
三点到直线![]() 的距离分别为:
的距离分别为:![]() ,
,
所以![]()
![]()
![]() .
.
所以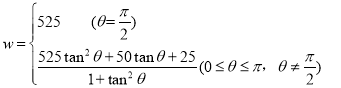
(2) 当直线![]() 的斜率不存在时,
的斜率不存在时,![]() =
=![]() ,
,
当直线![]() 的斜率存在时,
的斜率存在时,![]()
![]()
![]()
设![]() ,
,
当![]() 即
即![]() 时,
时,![]() =
=![]() .
.
当![]() 即
即![]() 时,
时,![]()
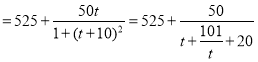 .
.
因为当![]() 时
时![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号)
当![]() 时,
时, ![]() (当且仅当
(当且仅当![]() 时取等号)
时取等号)
所以![]() 的最小值为
的最小值为![]()
此时![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目