Question

【题目】已知圆，圆，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C.

（1）求曲线C的方程；

（2）设不经过点的直线l与曲线C相交于A，B两点，直线QA与直线QB的斜率均存在且斜率之和为-2，证明：直线l过定点.

Answer 1

【答案】（1）；（2）证明见解析.

【解析】

（1）根据动圆P与圆M外切并且与圆N内切，得到，，从而得到，得到，从而求出椭圆的标准方程；（2）直线l斜率存在时，设，代入椭圆方程，得到，，表示出直线QA与直线QB的斜率，根据，得到，的关系，得到直线所过的定点，再验证直线l斜率不存在时，也过该定点，从而证明直线过定点.

（1）设动圆P的半径为r，

因为动圆P与圆M外切，所以，

因为动圆P与圆N内切，所以，

则，

由椭圆定义可知，曲线C是以为左、右焦点，长轴长为8的椭圆，

设椭圆方程为，

则，，故，

所以曲线C的方程为.

（2）①当直线l斜率存在时，设直线，，

联立，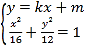

得，

设点，则，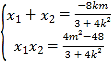

，

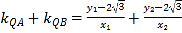
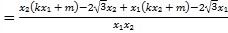
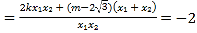所以，

即，

得.

则，

因为，所以.

即，

直线，

所以直线l过定点.

②当直线l斜率不存在时，设直线，且，

则点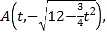

，

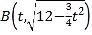
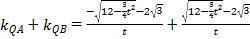
解得，

所以直线也过定点.

综上所述，直线l过定点.