题目内容
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
【答案】![]()
【解析】
试题根据题设条件,由(c﹣a)是(b﹣c)和(b﹣a)的等比中项,知[x(b﹣a)]2=(b﹣a)2﹣x(b﹣a)2,由此能求出最佳乐观系数x的值.
解:∵c﹣a=x(b﹣a),b﹣c=(b﹣a)﹣x(b﹣a),
(c﹣a)是(b﹣c)和(b﹣a)的等比中项,
∴[x(b﹣a)]2=(b﹣a)2﹣x(b﹣a)2,
∴x2+x﹣1=0,
解得![]() ,
,
∵0<x<1,
∴![]() .
.
故答案为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】数学是研究数量、结构、变化、空间以及信息等概念的一门科学.在人类历史发展和社会生活中,数学发挥着不可替代的作用,也是学习和研究现代科学技术必不可少的基本工具.
(1)为调查大学生喜欢数学命题是否与性别有关,随机选取![]() 名大学生进行问卷调查,当被调查者问卷评分不低于
名大学生进行问卷调查,当被调查者问卷评分不低于![]() 分则认为其喜欢数学命题,当评分低于
分则认为其喜欢数学命题,当评分低于![]() 分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
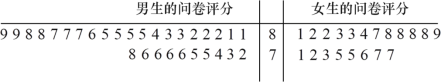
依据上述数据制成如下列联表:
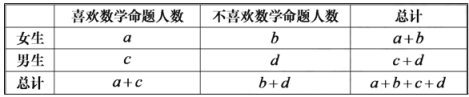
请问是否有![]() 的把握认为大学生是否喜欢数学命题与性别有关?
的把握认为大学生是否喜欢数学命题与性别有关?
参考公式及数据:![]() .
.
|
|
|
|
|
|
|
|
|
|
(2)在某次命题大赛中,![]() 同学要进行
同学要进行![]() 轮命题,其在每轮命题成功的概率均为
轮命题,其在每轮命题成功的概率均为![]() ,各轮命题相互独立,若该同学在
,各轮命题相互独立,若该同学在![]() 轮命题中恰有
轮命题中恰有![]() 次成功的概率为
次成功的概率为![]() ,记该同学在
,记该同学在![]() 轮命题中的成功次数为
轮命题中的成功次数为![]() ,求
,求![]() .
.
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行硏究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差x( | 8 | 11 | 13 | 12 | 10 |
发芽数y(颗) | 22 | 27 | 31 | 35 | 26 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均不小于27”的概率.
(2)若选取的是3月1日与3月5日的两组数据,请根据3月2日至3月4日的数据,求出y关于x的线性回归方程![]() .
.
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(参考公式:回归直线的方程是![]() ,其中
,其中 ,
,![]() )
)