题目内容
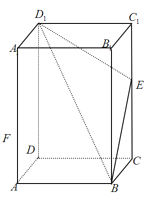
【题目】如图,已知在长方体![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上的一个动点,平面
上的一个动点,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,给出下列命题:
,给出下列命题:
①四棱锥![]() 的体积为
的体积为![]() ;
;
②存在唯一的点![]() ,使截面四边形
,使截面四边形![]() 的周长取得最小值
的周长取得最小值![]() ;
;
③当![]() 点不与
点不与![]() ,
,![]() 重合时,在棱
重合时,在棱![]() 上均存在点
上均存在点![]() ,使得
,使得![]() 平面
平面![]()
④存在唯一一点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]()
其中正确的命题是_____________(填写所有正确的序号)
【答案】①②④
【解析】
①根据![]() ,再根据等体积转化,求出
,再根据等体积转化,求出![]() 和
和![]() ,得到答案;②判断出截面四边形
,得到答案;②判断出截面四边形![]() 为平行四边形,将正方体侧面展开,面
为平行四边形,将正方体侧面展开,面![]() 和面
和面![]() 在同一平面内,得到
在同一平面内,得到![]() 最小为
最小为![]() 内
内![]() 的长度,从而得到截面四边形
的长度,从而得到截面四边形![]() 的周长的最小值;③取
的周长的最小值;③取![]() 为
为![]() 中点时,在平面
中点时,在平面![]() 中,延长
中,延长![]() ,交
,交![]() 于
于![]() ,可得
,可得![]() ;④以
;④以![]() 点建立空间直角坐标系,根据线面垂直,得到
点建立空间直角坐标系,根据线面垂直,得到![]() 点坐标,并求出
点坐标,并求出![]() .
.
长方体![]() 中,
中,![]()
命题①,![]()
易知![]() 平面
平面![]()
![]() 到平面
到平面![]() 的距离,等于
的距离,等于![]() 到平面
到平面![]() 的距离,为
的距离,为![]() ,
,
同理![]() 到平面
到平面![]() 的距离,等于
的距离,等于![]() 到平面
到平面![]() 的距离,为
的距离,为![]()
所以![]()
![]() ,故正确.
,故正确.
命题②,易知平面![]() 平面
平面![]() ,
,
平面![]()
![]() 平面
平面![]()
![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]()
所以![]() ,同理
,同理![]() ,
,
即四边形![]() 为平行四边形
为平行四边形
将正方体侧面展开,面![]() 和面
和面![]() 在同一平面内,
在同一平面内,
可得在![]() 内,
内,![]() 最小为
最小为![]() 的长度,
的长度,
此时![]() 点为
点为![]() 与
与![]() 的交点,
的交点,
![]()
所以四边形![]() 的周长取得最小值
的周长取得最小值![]() ,故正确.
,故正确.
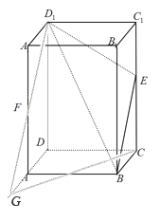
命题③,取![]() 为
为![]() 中点时,易知
中点时,易知![]() 为
为![]() 中点
中点
在平面![]() 中,延长
中,延长![]() ,交
,交![]() 于
于![]() ,
,
通过![]() ,得到
,得到![]() ,
,
所以![]() ,
,
即此时![]() 平面
平面![]() ,
,
而此时点![]() 在
在![]() 延长线上,不在棱
延长线上,不在棱![]() 上,故错误.
上,故错误.
命题④,以![]() 点建立空间直角坐标系,设点
点建立空间直角坐标系,设点![]()
![]() ,
,![]() ,
,![]()
所以![]() ,即
,即![]() ,
,
要使![]() 平面
平面![]() ,
,
则需![]() ,即
,即![]()
所以![]() ,得
,得![]() ,即
,即![]() ,故正确.
,故正确.
故答案为:①②④

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:,
![]() ;
;![]()
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
![]() Ⅰ
Ⅰ![]() 从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
![]() Ⅱ
Ⅱ![]() 根据以上
根据以上![]() 列联表,是否有
列联表,是否有![]() 以上的把握认为“性别与在选择座位时是否挑同桌”有关?
以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 参考公式:
参考公式: ![]() ,其中
,其中![]()