题目内容
【题目】已知数列{![]() }中,
}中,![]() ,且
,且![]() 对任意正整数都成立,数列{
对任意正整数都成立,数列{![]() }的前n项和为Sn。
}的前n项和为Sn。
(1)若![]() ,且
,且![]() ,求a;
,求a;
(2)是否存在实数k,使数列{![]() }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若![]() 。
。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
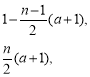
![]()
【解析】
试题分析:(1)![]() 时,
时,![]() ,由等差数列定义知数列
,由等差数列定义知数列![]() 是等差数列,由
是等差数列,由![]() 可得
可得![]() ,解得
,解得![]() ,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{
,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{![]() }是公比不为1,所以
}是公比不为1,所以![]() 不为等差中项,只需讨论
不为等差中项,只需讨论![]() 与
与![]() 为等差中项:若
为等差中项:若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得:![]() ,解得
,解得![]() (舍1);
(舍1);![]() ;同理若
;同理若![]() 为等差中项,
为等差中项,![]() (3)
(3)![]() 则
则![]() ,
,![]() ,从而
,从而![]() ,所以求和时要重新组合,每两项作为一组,先求
,所以求和时要重新组合,每两项作为一组,先求![]() 是偶数时,
是偶数时,![]()
![]()
![]() ,再求
,再求![]() 是奇数时,
是奇数时,![]()
![]()
![]()
![]()
![]() ,
,
试题解析:(1)![]() 时,
时,![]() ,
,![]() ,所以数列
,所以数列![]() 是等差数列 1分
是等差数列 1分
此时首项![]() ,公差
,公差![]() ,数列
,数列![]() 的前
的前![]() 项和是
项和是![]() 3分
3分
故![]() ,即
,即![]() ,得
,得![]() ; 4分
; 4分
(没有过程,直接写![]() 不给分)
不给分)
(2)设数列![]() 是等比数列,则它的公比
是等比数列,则它的公比![]() ,所以
,所以![]() ,
,![]() ,
,![]() 6分
6分
①若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,解得:
,解得:![]() ,不合题意;
,不合题意;
②若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得:![]() ,
,
解得![]() (舍1);
(舍1);![]() ;
;
③若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得:![]() ,
,
解得![]() ;
;![]() ; 9分
; 9分
综上可得,满足要求的实数![]() 有且仅有一个,
有且仅有一个,![]() ; 10分
; 10分
(3)![]() 则
则![]() ,
,
![]() ,
,![]() , 12分
, 12分
当![]() 是偶数时,
是偶数时,
![]()
![]()
![]() ,
,
当![]() 是奇数时,
是奇数时,
![]()
![]()
![]()
![]()
![]() ,
,![]() 也适合上式, 15分
也适合上式, 15分
综上可得,![]()
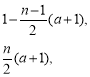
![]() . 16分
. 16分

练习册系列答案
相关题目
【题目】某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这种服装件数x之间的一组数据关系如下表
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获纯利多少元?
已知: ![]() x
x ![]() =280,
=280, ![]() y
y ![]() =45309,
=45309, ![]() xiyi=3487,
xiyi=3487, ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.