题目内容
【题目】设抛物线y2=2x的焦点为F,过点M( ![]() ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,|BF|=2,则△BCF和△ACF的面积之比为 .
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于C,|BF|=2,则△BCF和△ACF的面积之比为 .
【答案】![]()
【解析】解:∵抛物线方程为y2=2x,∴焦点F的坐标为( ![]() ,0), 准线方程为x=﹣
,0), 准线方程为x=﹣ ![]() ,
,
如图,设A(x1 , y1),B(x2 , y2),
过A,B分别向抛物线的准线作垂线,垂足分别为E,N,
则|BF|=x2+ ![]() =2,
=2,
∴x2= ![]() ,
,
把x2= ![]() 代入抛物线y2=2x,得,y2=﹣
代入抛物线y2=2x,得,y2=﹣ ![]() ,
,
∴直线AB过点M( ![]() ,0)与(
,0)与( ![]() ,﹣
,﹣ ![]() )
)
方程为 ![]() x+(
x+( ![]() ﹣
﹣ ![]() )y﹣3=0,代入抛物线方程,解得,x1=2
)y﹣3=0,代入抛物线方程,解得,x1=2
∴|AE|=2+ ![]() =
= ![]() ,
,
∵在△AEC中,BN∥AE,
∴|BC|:|AC|=|BN|:|AE|=2: ![]() =
= ![]() ,
,
△BCF和△ACF的面积之比为: ![]() |BC|h:
|BC|h: ![]() |AC|h=
|AC|h= ![]()
所以答案是: ![]()

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
【题目】某地区2009年至2015年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2009年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 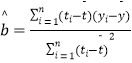 .
. ![]() .
.
参考数据:(﹣3)×(﹣1.4)+(﹣2)×(﹣1)+(﹣1)×(﹣0.7)+1×0.5+2×0.9+3×1.6=14.