Question

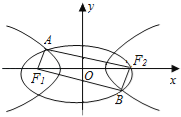
【题目】如图所示,已知☉O1与☉O2相交于A,B两点,过点A作☉O1的切线交☉O2于点C,过点B作两圆的割线,分别交☉O1、☉O2于点D、E,DE与AC相交于点P.若AD是☉O2的切线,且PA=6,PC=2,BD=9,则AB的长为____.

Answer 1

【答案】6

【解析】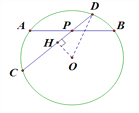

试题分析：由 与 相切 ,再由切割线定理得

,再相交弦定理知 ,又由切割线定理可得 易证 , 所以 .

试题解析：因为AC与☉O1相切,切点为A,所以∠BAC=∠ADB,

又∠BAC=∠BEC,所以∠ADB=∠BEC.所以AD∥CE,所以△CPE∽△APD,

所以,即CE=AD,因为AP为☉O1的切线,PBD为☉O1的割线,所以由切割线定理得PA2=PB·PD=PB·(PB+BD),即36=PB·(PB+9),解得,在☉O2中,由相交弦定理知PB·PE=PA·PC,即3PE=2×6,得PE=4,又因为AD为☉O2的切线,DBE为☉O2的割线,所以由切割线定理可得DA2=DB·DE,即DA2=9×(9+3+4),得DA=12,所以CE=4.

易证△BPA∽△CPE,所以,所以AB=CE=6.