题目内容
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n∈N +),其中xn为正实数.
(1)用xn表示xn+1;
(2)若x1=4,记an=lg ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(3)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
(1)用xn表示xn+1;
(2)若x1=4,记an=lg
 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;(3)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
(1) ;(2)
;(2) ;(3)详见解析.
;(3)详见解析.
 ;(2)
;(2) ;(3)详见解析.
;(3)详见解析.试题分析:(1)由题设条件知曲线y=f(x)在点
 处的切线方程是
处的切线方程是 .由此可知
.由此可知 .所以
.所以 .(2)由
.(2)由 ,知
,知 ,同理
,同理 .故
.故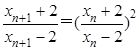 .由此入手能够导出
.由此入手能够导出 .(3)由题设知
.(3)由题设知 ,所以
,所以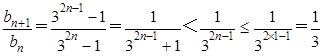 ,由此可知
,由此可知 .
.解:(1)由题可得
 .
.所以曲线
 在点
在点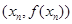 处的切线方程是:
处的切线方程是: .
.即
 .
.令
 ,得
,得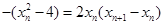 .
.即
 .显然
.显然 ,
,∴
 .
.(2)由
 ,知
,知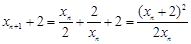 ,’同理
,’同理 .----6’
.----6’故
 .-----7’
.-----7’从而
 ,即
,即 .所以,数列
.所以,数列 成等比数列.---8’
成等比数列.---8’故
 .即
.即 .----9’
.----9’从而
 ,所以
,所以 .----10’
.----10’(3)由(Ⅱ)知
 ,∴
,∴
∴
 ---11’
---11’当
 时,显然
时,显然 .-------12’
.-------12’当
 时,
时, -----13’
-----13’∴



 .综上,
.综上,
 .
.
练习册系列答案
相关题目
 在点(1,-1)处的切线方程为( )
在点(1,-1)处的切线方程为( ) 中,已知P是函数
中,已知P是函数 (x>0)的图象上的动点,该图象在点P处的切线
(x>0)的图象上的动点,该图象在点P处的切线 交y轴于点M,过点P作
交y轴于点M,过点P作 ,则
,则 .
. 的单调性;
的单调性; 的图象在点(2,f(2))处的切线的倾斜角为
的图象在点(2,f(2))处的切线的倾斜角为 ,对于任意的
,对于任意的 ,函数
,函数 在区间(t,3)上总不是单调函数,求m的取值范围;
在区间(t,3)上总不是单调函数,求m的取值范围; 上可导的任意函数
上可导的任意函数 ,若满足
,若满足 ,则必有( ).
,则必有( ).


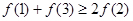
 :
:
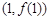 处的切线方程;
处的切线方程; 平行的曲线C的切线方程.
平行的曲线C的切线方程. 的导数
的导数 ,则数列
,则数列 的前n项和( )
的前n项和( )



 ,则
,则 ( )
( )