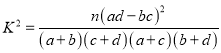题目内容
【题目】某人上午7时,乘摩托艇以匀速vkm/h(8≤v≤40)从A港出发到距100km的B港去,然后乘汽车以匀速wkm/h(30≤w≤100)自B港向距300km的C市驶去.应该在同一天下午4至9点到达C市. 设乘坐汽车、摩托艇去目的地所需要的时间分别是xh,yh.
(1)作图表示满足上述条件的x,y范围;
(2)如果已知所需的经费p=100+3(5﹣x)+2(8﹣y)(元),那么v,w分别是多少时p最小?此时需花费多少元?
【答案】
(1)解:依题意得 ![]() ,∴
,∴ ![]() ①
①
由于乘汽车、摩托艇所需的时间和x+y应在9至 14个小时之间,即9≤x+y≤14②
因此,满足①②的点(x,y)的存在范围是图中阴影部分(包括边界)
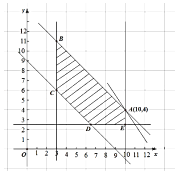
(2)解:∵p=100+3(5﹣x)+2(8﹣y)=131﹣3x﹣2y,上式表示斜率为 ![]() 的直线,
的直线,
当动直线p=131﹣3x﹣2y通过图中的阴影部分区域(包括边界),通过点A时,p值最小.
由 ![]() 得
得 ![]() ,即当x=10,y=4时,p最小.
,即当x=10,y=4时,p最小.
此时,v=25,w=30,p的最小值为 93元
【解析】(1)由路程,速度,时间的关系得出x,y与v,w的关系式,由v,w得范围即可得x,y的范围,再由到达时间范围即可得到不等式组,作图即可;(2)利用线性规划知识易求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目