题目内容
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,![]() 获得本场比赛胜利,最终人机大战总比分定格在
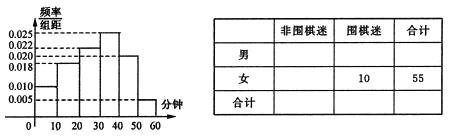
获得本场比赛胜利,最终人机大战总比分定格在![]() .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(1)根据已知条件完成如图列联表,并据此资料判断你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.010 |
| 3.74 | 6.63 |
【答案】见解析.
【解析】
试题分析:(1)根据频率分布直方图补充![]() 列联表,再将
列联表,再将![]() 列联表中的数据代入公式计算即可;
列联表中的数据代入公式计算即可;
(2)依题意得到![]() ,可以写出
,可以写出![]() 的分布列,再进行计算即可。
的分布列,再进行计算即可。
试题解析:
(1)由频率分布直方图可知,在抽取的100人中,“围棋迷”有25人,
从而![]() 列联表如下:
列联表如下:
非围棋迷 | 围棋迷 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
将![]() 列联表中的数据代入公式计算,得
列联表中的数据代入公式计算,得
![]()
因为![]() ,所以没有理由认为“围棋迷”与性别有关.
,所以没有理由认为“围棋迷”与性别有关.
(2)由频率分布直方图知抽到“围棋迷”的频率为![]() ,将频率视为概率,即从观众中抽取一名“围棋迷”的概率为
,将频率视为概率,即从观众中抽取一名“围棋迷”的概率为![]() .由题意
.由题意![]() ,从而
,从而![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() ,
,![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 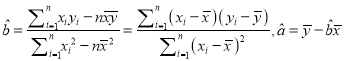 )
)
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
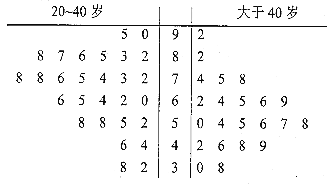
(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,记抽到的2人中年龄大于40岁的市民人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() .
.
