题目内容
2．已知函数f（x）=|x+1|+|x-4|．（1）求不等式f（x）≤7的解集；
（2）若存在x0∈R，使得f（x0）≤|2a+3|成立，求实数a的取值范围．
分析 （1）由条件利用绝对值的意义求得不等式f（x）≤7的解集．
（2）由题意可得f（x）≤|2a+3|有解，故f（x）=|x+1|+|x-4|的最小值5≤|2a+3|，可得2a+3≥5 或2a+3≤-5，求得a的范围．
解答 解：（1）函数f（x）=|x+1|+|x-4|表示数轴上的x对应点到-1、4对应点的距离之和，
而-2和5对应点到-1、4对应点的距离之和正好等于7，故不等式f（x）≤7的解集为[-2，5]．
（2）由题意可得f（x）≤|2a+3|有解，故f（x）=|x+1|+|x-4|的最小值5≤|2a+3|，
故2a+3≥5 或2a+3≤-5，求得a≥2或 a≤-4，
故a的范围是{a|a≥2或 a≤-4 }．
点评 本题主要考查绝对值的意义，绝对值不等式的解法，函数的能成立问题，属于中档题．
练习册系列答案
相关题目
12．焦点为（0，±3），且与双曲线$\frac{x^2}{2}-{y^2}=1$有相同的渐近线的双曲线方程是（ ）
| A． | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | B． | $\frac{y^2}{3}-\frac{x^2}{6}=1$ | C． | $\frac{y^2}{6}-\frac{x^2}{3}=1$ | D． | $\frac{x^2}{6}-\frac{y^2}{3}=1$ |
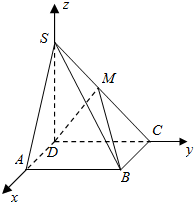如图，在四棱锥S-ABCD中，底面ABCD为矩形，SD⊥底面ABCD，AD=$\sqrt{2}$，DC=SD=2，点M在侧棱SC上，∠ABM=60°．若以DA，DC，DS，分别为x轴，y轴，z轴建立如图所示的空间直角坐标系D-xyz，则M的坐标为（0，1，1）．
7．已知一条直线与一个平面内的两条直线垂直．则该直线与这个平面的位置关系为（ ）
| A． | 平行 | B． | 相交 | C． | 在平面内 | D． | 都有可能 |
14．函数y=$5\sqrt{x-1}+\sqrt{2}•\sqrt{5-x}$最大值为（ ）
| A． | 108 | B． | $6\sqrt{3}$ | C． | 10 | D． | 27 |