题目内容
1．有一个角为60°的钝角三角形，满足最大边与最小边之比为m，则m的取值范围为（2，+∞）．分析 设钝角三角形的三内角为：60°-α，60°，60°+α，则90°＜60°+α＜120°，求出α的范围，由正弦定理求得tanα=$\frac{\sqrt{3}（m-1）}{m+1}$．再由tanα的范围解不等式求出m的取值范围．
解答 解：设钝角三角形的三内角为：60°-α，60°，60°+α，
则90°＜60°+α＜120°，
即30°＜α＜60°，设60°+α对应a边，60°-α对应b边，
由正弦定理，得：$\frac{a}{b}$=$\frac{sin（60°+α）}{sin（60°-α）}$=$\frac{sin60°cosα+cos60°sinα}{sin60°cosα-cos60°sinα}$=m，
∴tanα=$\frac{\sqrt{3}（m-1）}{m+1}$．
∵30°＜α＜60°，
∴$\frac{\sqrt{3}}{3}$＜tanα＜$\sqrt{3}$，
∴m＞2，
故m的取值范围为（2，+∞）．
点评 本题考查等差数列的定义和性质，正弦定理的应用，求得tanα=$\frac{\sqrt{3}（m-1）}{m+1}$是解题的关键，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．
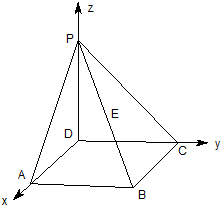PD垂直于正方形ABCD所在平面，AB=2，E为PB的中点，cos＜$\overrightarrow{DP}$，$\overrightarrow{AE}$＞=$\frac{\sqrt{3}}{3}$，若以如图所示建立空间直角坐标系，则E点坐标为（ ）
PD垂直于正方形ABCD所在平面，AB=2，E为PB的中点，cos＜$\overrightarrow{DP}$，$\overrightarrow{AE}$＞=$\frac{\sqrt{3}}{3}$，若以如图所示建立空间直角坐标系，则E点坐标为（ ）| A． | （1，1，2） | B． | （2，2，1） | C． | （1，1，1） | D． | $（1\;，\;1\;，\;\frac{1}{2}）$ |
6．若函数y=f（x）在点x=1处的导数为1，则$\underset{lim}{△x→0}$$\frac{f（1+△x）-f（x）}{△x}$=（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
10．在△ABC中，已知a=40，b=20$\sqrt{2}$，A=45°，则角B等于（ ）
| A． | 60° | B． | 60°或120° | C． | 30° | D． | 30°或150° |