题目内容
16.函数y=$\sqrt{2-x}$+1g(x-1)的定义域是(1,2].分析 通过对数的真数大于0,被开偶次方数非负求解即可.
解答 解:要使函数有意义,可得:$\left\{\begin{array}{l}2-x≥0\\ x-1>0\end{array}\right.$,解得:x∈(1,2].
函数y=$\sqrt{2-x}$+1g(x-1)的定义域是(1,2].
故答案为:(1,2].
点评 本题考查函数的定义域的求法,对数的解得性质的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
| A. | 模型1的相关指数R2为0.50 | B. | 模型2的相关指数R2为0.80 | ||
| C. | 模型3的相关指数R2为0.90 | D. | 模型4的相关指数R2为0.25 |
7.过原点的直线与圆x2+y2-6x+5=0相交于A,B两点,则弦AB的中点M的轨迹方程为( )
| A. | x2+y2+3x=0 | B. | x2-y2-3x=0 | C. | x2-y2+3x=0 | D. | x2+y2-3x=0 |
8.若抛物线y=ax2在点x=1处的切线与直线x+2y=0垂直,则a=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
5.函数f(x)=x3+bx2+cx+d的图象如图所示,则函数g(x)=log2(x2+$\frac{2b}{3}$+$\frac{c}{3}$)的单调递减区间是( )
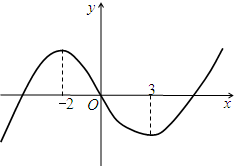

| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
6.8名学生和2位老师站成一排合影,2位老师恰好相邻的排法种数为( )
| A. | A${\;}_{9}^{9}$A${\;}_{2}^{2}$ | B. | A${\;}_{9}^{9}$ | C. | A${\;}_{10}^{10}$ | D. | 2A${\;}_{10}^{9}$ |