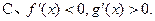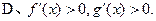题目内容
(本小题满分12分)
关于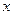 的函数
的函数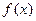 与数列
与数列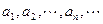 具有关系:
具有关系:
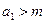 ,
,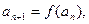 (
(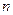 =1,2,3,…)(
=1,2,3,…)(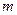 为常数),又设函数
为常数),又设函数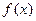 的导数
的导数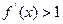 ,
,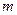 为方程
为方程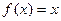 的实根.
的实根.
(I)用数学归纳法证明: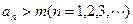 ;
;
(II)证明: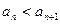 .
.
关于
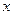 的函数
的函数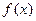 与数列
与数列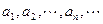 具有关系:
具有关系: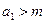 ,
,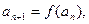 (
(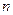 =1,2,3,…)(
=1,2,3,…)(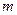 为常数),又设函数
为常数),又设函数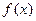 的导数
的导数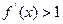 ,
,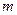 为方程
为方程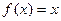 的实根.
的实根.(I)用数学归纳法证明:
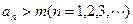 ;
;(II)证明:
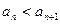 .
.(Ⅰ)证明:当n=1,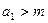 成立
成立
假设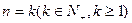 时,
时,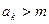 成立.
成立.
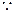
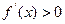 ,可见函数
,可见函数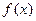 是单调递增函数.
是单调递增函数.
当n=k+1时,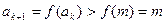 .
.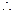 n=k+1时命题成立。
n=k+1时命题成立。
综上,对一切正整数n ,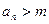 成立. ………6分
成立. ………6分
(Ⅱ)为证明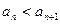
 ,只需证明
,只需证明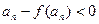 即可.
即可.
令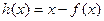 ,
,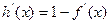
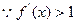 ,
, ,h(x)是单调减函数,而h(m)=m-f(m)=0
,h(x)是单调减函数,而h(m)=m-f(m)=0
又 an>m ,h(an)=an-f(an)<0,所以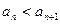 . ………12分
. ………12分
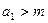 成立
成立假设
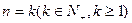 时,
时,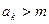 成立.
成立.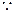
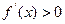 ,可见函数
,可见函数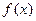 是单调递增函数.
是单调递增函数.当n=k+1时,
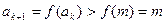 .
.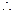 n=k+1时命题成立。
n=k+1时命题成立。综上,对一切正整数n ,
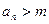 成立. ………6分
成立. ………6分(Ⅱ)为证明
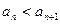
 ,只需证明
,只需证明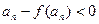 即可.
即可.令
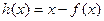 ,
,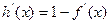
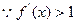 ,
, ,h(x)是单调减函数,而h(m)=m-f(m)=0
,h(x)是单调减函数,而h(m)=m-f(m)=0又 an>m ,h(an)=an-f(an)<0,所以
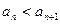 . ………12分
. ………12分略

练习册系列答案
相关题目
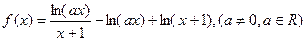 .
.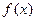 的定义域;
的定义域;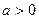 时,若存
时,若存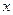 在使得
在使得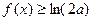 成立,求
成立,求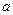 的取值范围.
的取值范围.
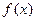 =
=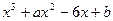 ,
, 、
、 为实数,
为实数,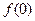 =1,
=1,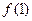 )处切线的斜率为-6。
)处切线的斜率为-6。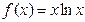
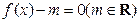 的解的个数;
的解的个数;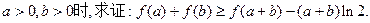
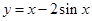 ,
,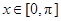 的单调递增区间是 .
的单调递增区间是 .