题目内容
(12分) 已知三次函数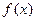 =
=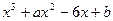 ,
, 、
、 为实数,
为实数,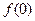 =1,
=1,
曲线y=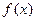 在点(1,
在点(1,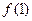 )处切线的斜率为-6。
)处切线的斜率为-6。
(1)求函数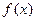 的解析式;
的解析式;
(2)求函数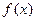 在(-2,2)上的最大值
在(-2,2)上的最大值
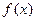 =
=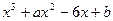 ,
, 、
、 为实数,
为实数,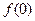 =1,
=1,曲线y=
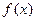 在点(1,
在点(1,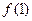 )处切线的斜率为-6。
)处切线的斜率为-6。(1)求函数
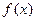 的解析式;
的解析式;(2)求函数
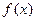 在(-2,2)上的最大值
在(-2,2)上的最大值解:(1)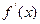 =
=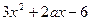
由导数的几何意义,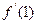 =-6 ∴
=-6 ∴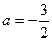
∵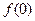 =1 ∴
=1 ∴ 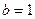
∴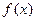 =
=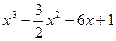 ………………6分
………………6分
(2)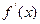 =
=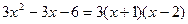
令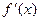 =0得
=0得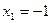 ,
,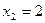
当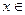 (-2,-1)时,
(-2,-1)时,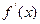 >0,
>0,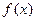 递增;
递增;
当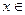 (-1,2)时,
(-1,2)时,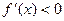 ,
,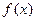 递减。
递减。
∴ 在区间(-2,2)内,函数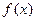 的最大值为
的最大值为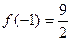 ……
…… …………12分
…………12分
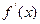 =
=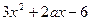
由导数的几何意义,
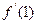 =-6 ∴
=-6 ∴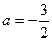
∵
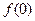 =1 ∴
=1 ∴ 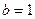
∴
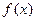 =
=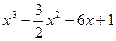 ………………6分
………………6分(2)
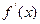 =
=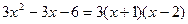
令
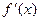 =0得
=0得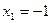 ,
,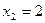
当
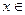 (-2,-1)时,
(-2,-1)时,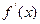 >0,
>0,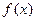 递增;
递增;当
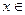 (-1,2)时,
(-1,2)时,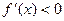 ,
,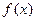 递减。
递减。∴ 在区间(-2,2)内,函数
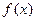 的最大值为
的最大值为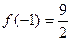 ……
…… …………12分
…………12分略

练习册系列答案
相关题目
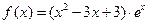 定义域为
定义域为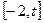 (
(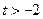 ),设
),设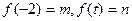 .
.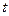 的取值范围,使得函数
的取值范围,使得函数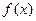 在
在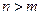 ;
;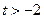 ,总存在
,总存在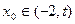 ,满足
,满足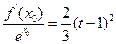 ,并确定这样的
,并确定这样的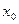 的个数.
的个数.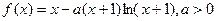 .
.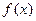 的单调区间;
的单调区间;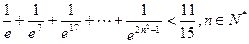 .
.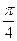 .
. ?若存在,求出最小的正整数k,否则请说明理由.
?若存在,求出最小的正整数k,否则请说明理由.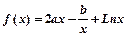
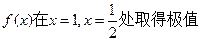 ,
, 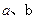 的值;
的值;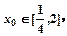 使得不等式
使得不等式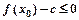 成立,求
成立,求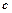 的最小值;
的最小值;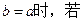
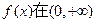 上是单调函数,求
上是单调函数,求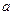 的取值范围。
的取值范围。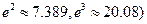
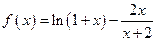 ,证明:当
,证明:当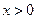 时,
时,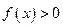
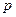 ,证明:
,证明: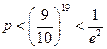
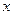 的函数
的函数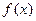 与数列
与数列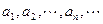 具有关系:
具有关系: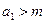 ,
,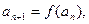 (
(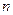 =1,2,3,…)(
=1,2,3,…)(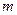 为常数),又设函数
为常数),又设函数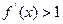 ,
,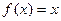 的实根.
的实根.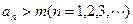 ;
;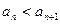 .
.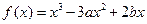 在点
在点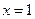 处有极小值
处有极小值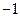 ,试确定
,试确定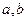 的值,并求出
的值,并求出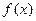 的单调区间。
的单调区间。