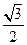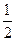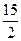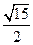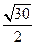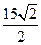题目内容
等边ABC的A∈平面α，B、C到面α的距离分别为2a、a，且AB=BC=AC=b.
(1)求面ABC与α所成二面角的大小；
(2)若B、C到α的距离分别为3a、a呢?
(1)求面ABC与α所成二面角的大小；
(2)若B、C到α的距离分别为3a、a呢?
（1）∠BAG=arcsin
（2）arcsin
(1)延长BD交α于D B、C在α上的射影为G、H.则
G、H、D共线 BG="2GH " ∴BC=CD
∴∠BAD=90°,GA⊥AD,∠BAG为所求.
sin∠BAC=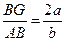
∠BAG=arcsin
(2)
=3
∴BC="2CD " CD=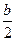
AD2=AC2+CD2+AC·CD=
∴AD=
b
C到AD的距离为
设所成角为α，则
sinα=
α=arcsin
G、H、D共线 BG="2GH " ∴BC=CD
∴∠BAD=90°,GA⊥AD,∠BAG为所求.
sin∠BAC=
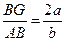∠BAG=arcsin(2)
=3∴BC="2CD " CD=
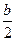
AD2=AC2+CD2+AC·CD=
∴AD=bC到AD的距离为
设所成角为α，则
sinα=
α=arcsin
练习册系列答案
相关题目
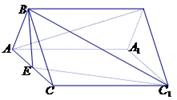
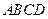和矩形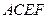
所在的平面互相垂直，
，
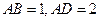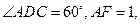
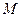是线段
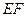的中点.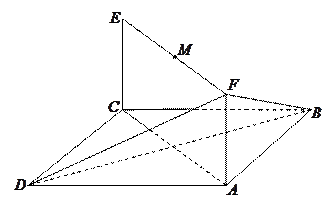
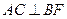；（2）求二面角
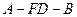的大小；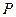
为一动点，若点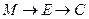
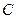，求这一过程中形成的三棱锥
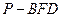的体积的最小值.
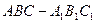中，
.
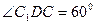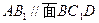（5分）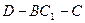
的大小。（7分）
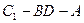平面角的大小。（7分）
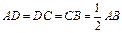，E是AB的中点，将△ADE沿DE折起，使点A折到点P的位置，且二面角
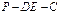的大小为1200．
；
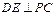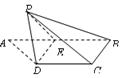
是直角梯形，
，
，
，
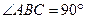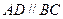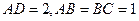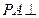平面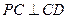
；
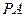上是否存在一点
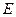，使得
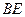∥平面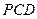
？若存在，找出点
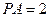，求二面角
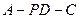的余弦值．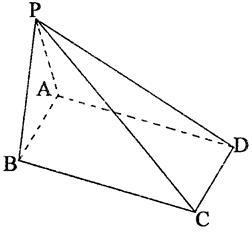
.
；
；
.
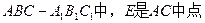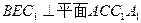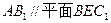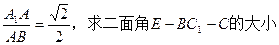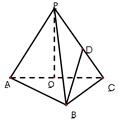
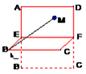
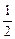，那么点M到直线EF的距离为( )
