题目内容
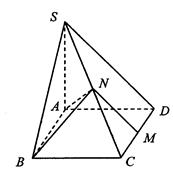
如图,梯形ABCD中,CD//AB,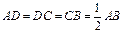 ,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角
,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角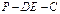 的大小为1200.
的大小为1200.
(I)求证: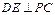 ;
;
(II)求直线PD与平面BCDE所成角的大小;
(III)求点D到平面PBC的距离.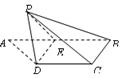
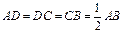 ,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角
,E是AB的中点,将△ADE沿DE折起,使点A折到点P的位置,且二面角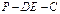 的大小为1200.
的大小为1200.(I)求证:
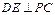 ;
;(II)求直线PD与平面BCDE所成角的大小;
(III)求点D到平面PBC的距离.

I)证明见解析 (II)直线PD与平面BCDE所成角是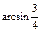 .
.
(III)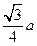 .
.
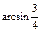 .
.(III)
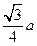 .
.(I)连结AC交DE于F,连结PF.
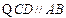 ,
,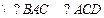 .
.
又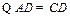 ,
,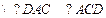 ,
,
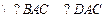 ,
,
即CA平分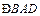 .
.
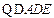 是正三角形,
是正三角形,
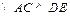 ,即PF⊥DE,CF⊥DE,
,即PF⊥DE,CF⊥DE,
∴DE⊥面PCF,∴DE⊥PC.
(II)过P作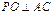 于O,连结OD,设AD = DC = CB = a,则AB = 2a,
于O,连结OD,设AD = DC = CB = a,则AB = 2a,
∵DE⊥面PCF,∴DE⊥PO,
∴PO⊥面BCDE,
∴∠PDO就是直线PD与平面BCDE所成的角.
∵∠PFC是二面角P-DE-C的平面角,
∴∠PFO= 60°,在RT△POD中,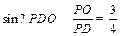 ,
,
 直线PD与平面BCDE所成角是
直线PD与平面BCDE所成角是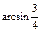 .
.
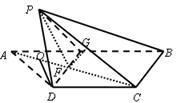
(III)∵DE∥BC,DE在平面PBC外, ,
,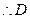 点到面
点到面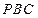 的距离即为点F到面PBC的距离,过点F作FG⊥PC,垂足为G.
的距离即为点F到面PBC的距离,过点F作FG⊥PC,垂足为G.
∴DE⊥面PCF,
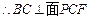 .
.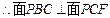 ,
,
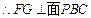 ,
,
∴FG的长即为点F到面PBC的距离.
在菱形ADCE中,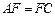 ,
,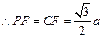 .
.
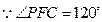 ,
,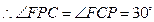 ,
,
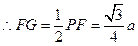 .
.
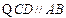 ,
,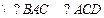 .
.又
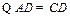 ,
,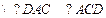 ,
,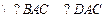 ,
,即CA平分
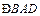 .
. 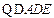 是正三角形,
是正三角形,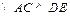 ,即PF⊥DE,CF⊥DE,
,即PF⊥DE,CF⊥DE,∴DE⊥面PCF,∴DE⊥PC.
(II)过P作
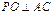 于O,连结OD,设AD = DC = CB = a,则AB = 2a,
于O,连结OD,设AD = DC = CB = a,则AB = 2a,∵DE⊥面PCF,∴DE⊥PO,
∴PO⊥面BCDE,
∴∠PDO就是直线PD与平面BCDE所成的角.
∵∠PFC是二面角P-DE-C的平面角,
∴∠PFO= 60°,在RT△POD中,
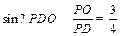 ,
, 直线PD与平面BCDE所成角是
直线PD与平面BCDE所成角是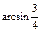 .
.
(III)∵DE∥BC,DE在平面PBC外,
 ,
, 点到面
点到面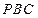 的距离即为点F到面PBC的距离,过点F作FG⊥PC,垂足为G.
的距离即为点F到面PBC的距离,过点F作FG⊥PC,垂足为G.∴DE⊥面PCF,
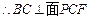 .
.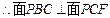 ,
,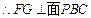 ,
,∴FG的长即为点F到面PBC的距离.
在菱形ADCE中,
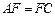 ,
,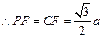 .
.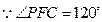 ,
,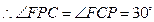 ,
,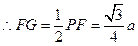 .
.
练习册系列答案
相关题目
 的正方体
的正方体 中,
中,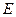 为棱
为棱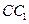 的中点.
的中点.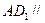 平面
平面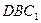 ; (Ⅱ)求
; (Ⅱ)求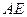 与平面
与平面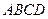 所成角的余弦值.
所成角的余弦值.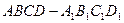 的棱长为2
的棱长为2 ,E为AB的中点.(Ⅰ)求证:
,E为AB的中点.(Ⅰ)求证: (Ⅱ)求异面直线BD1与CE所成角的余弦值;(Ⅲ)求点B到平面
(Ⅱ)求异面直线BD1与CE所成角的余弦值;(Ⅲ)求点B到平面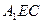 的距离.
的距离.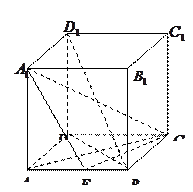

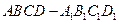 中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA
中,底面ABCD为等腰梯形,AB∥CD,AB="4,BC=CD=2," AA ="2, " E、E
="2, " E、E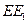 ∥平面
∥平面 ;
; 

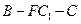 的余弦值
的余弦值
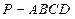 中,
中,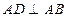 ,
,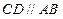 ,
,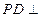 底面
底面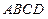 ,
, 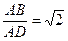 ,直线
,直线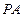 与底面
与底面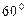 角,点
角,点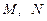 分别是
分别是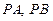 的中点.
的中点.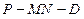 的大小;
的大小;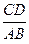 的值为多少时,
的值为多少时, 为直角三角形.
为直角三角形.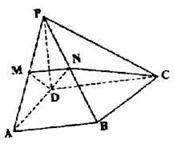
 ∶1,F是AB的中点.
∶1,F是AB的中点.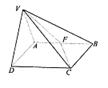
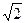 .
.