题目内容
若数列{an}存在一个常数M,使得对任意的n∈N*,都有|an|≤M,则称{an}是有界数列,下列数列中不是有界数列的是( )
| A.an=2+sinnx | B.an=
| |||||||||||
C.an=(
| D.an=
|
A.对于?x∈R,则|sinx|≤1,∴|an|≤2+|sinx|=3,{an}是有界数列;
B.an=
是关于n的单调递减数列,∴|an|=an≤a1=
,{an}是有界数列;
C.由于(
)n与(
)n都是单调递减数列,
∴|an|=an≤
+
+1=
.∴{an}是有界数列;
D.当n=2k-1时,|an|=|(-2)n|=2n是一个无界数列.
综上可知:只有D是一个无界数列.
故选:D.
B.an=
| 1 |
| 2n |
| 1 |
| 2 |
C.由于(
| 1 |
| 4 |
| 1 |
| 2 |
∴|an|=an≤
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
D.当n=2k-1时,|an|=|(-2)n|=2n是一个无界数列.
综上可知:只有D是一个无界数列.
故选:D.

练习册系列答案
相关题目
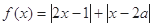 .
.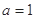 时,求
时,求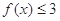 的解集;
的解集;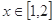 时,
时,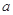 的集合.
的集合. (
( +
+ +
+ ).
). .
. ,比较
,比较 与
与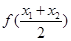 的大小;
的大小; 时,有
时,有 ,求实数
,求实数 的取值范围.
的取值范围.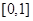 上的函数
上的函数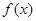 满足:
满足: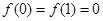 ;
;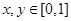 ,且
,且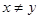 ,有
,有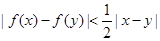 .
.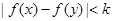 ,则k的最小值为( )
,则k的最小值为( )

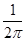

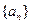 ,
,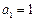 ,
,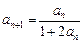 (
(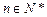 ),写出这个数列的前4项,并根据规律,写出这个数列的一个通项公式.
),写出这个数列的前4项,并根据规律,写出这个数列的一个通项公式.