题目内容
已知a,b,c为互不相等的非负数,求证:a2+b2+c2> (
( +
+ +
+ ).
).
 (
( +
+ +
+ ).
).见解析
试题分析:因为a,b,c为互不相等的非负数,由重要不等式得,a2+b2>2ab,b2+c2>2bc,a2+c2>2ac,利用同向不等式的加法原则得,a2+b2+c2>ab+bc+ac,由基本不等式得ab+bc>2
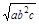 ,bc+ac>2
,bc+ac>2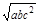 ,ab+ac>2
,ab+ac>2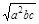 ,再利用加法原则得,ab+bc+ac>
,再利用加法原则得,ab+bc+ac> (
( +
+ +
+ ),再利用不等式的传递性即得所要证明的结论.
),再利用不等式的传递性即得所要证明的结论.试题解析:证明 ∵a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac.
又∵a,b,c为互不相等的非负数,
∴上面三个式子中都不能取“=”,
∴a2+b2+c2>ab+bc+ac,
∵ab+bc≥2
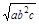 ,bc+ac≥2
,bc+ac≥2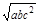 ,
,ab+ac≥2
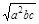 ,
,又a,b,c为互不相等的非负数,
∴ab+bc+ac>
 (
( +
+ +
+ ),
),∴a2+b2+c2>
 (
( +
+ +
+ ) (14分)
) (14分)
练习册系列答案
相关题目
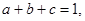
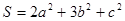 的最小值及取最小值时
的最小值及取最小值时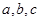 的值。
的值。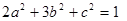 ,求
,求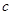 的取值范围。
的取值范围。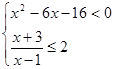
 ,
, ,则
,则 与
与 的大小关系为 .
的大小关系为 . 的不等式
的不等式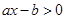 的解集是
的解集是 ,则关于
,则关于 的解( )
的解( )


