题目内容

已知数列{an}中，a1=1，2nan+1=（n+1）an，则数列{an}的通项公式为（　　）
A．
n
2n
B．
n
2n-1
C．
n
2n-1
D．
n+1
2n
∵2nan+1=（n+1）an，
∴
an+1
n+1
=
1
2
•
an
n
，
∴数列{
an
n
}是等比数列，首项
a1
1
=1，公比为
1
2
．
∴
an
n
=(
1
2
)n-1，
∴an=
n
2n-1
．
故选：B．
练习册系列答案
相关题目
数列
3
，3，
15
，
21
，3
3
，…，则9是这个数列的第（　　）
A．12项B．13项C．14项D．15项
设数列{an}满足an=
bn-b-4(n≤3)
log2n(n＞3)
（n∈N+），若数列{an}是递增数列，则b的范围是（　　）
A．（0，3）B．（0，2+
1
2
log23）
C．（1，3]D．（0，2+
1
2
log23]
已知数列{an}的通项公式是an=2+
200-30n
n2
，则数列{an}中最小项的项数是第______项．
若数列{an}存在一个常数M，使得对任意的n∈N*，都有|an|≤M，则称{an}是有界数列，下列数列中不是有界数列的是（　　）
A．an=2+sinnxB．an=
1
2n
C．an=(
1
4
)n+(
1
2
)n+1		D．an=
1
n
，n=2k
(-2)n，n=2k-1
解不等式组
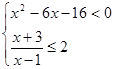
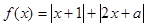若函数的最小值3，则实数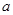的值为（   ）
A．5或8B．或5C．或D．或
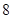
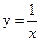已知数列{an}的图像是函数图像上，当x取正整数时的点列，则其通项公式为       。
已知关于的不等式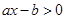的解集是，则关于的不等式的解(     )
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网