题目内容
已知函数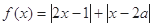 .
.
(1)当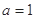 时,求
时,求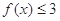 的解集;
的解集;
(2)当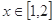 时,
时,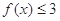 恒成立,求实数
恒成立,求实数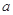 的集合.
的集合.
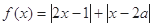 .
.(1)当
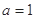 时,求
时,求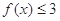 的解集;
的解集;(2)当
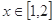 时,
时,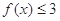 恒成立,求实数
恒成立,求实数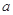 的集合.
的集合.(1)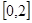 ;(2)
;(2)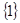 .
.
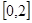 ;(2)
;(2)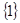 .
.试题分析:
解题思路:(1)利用
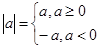 ,去掉绝对值符号进行求解(2)先根据所给范围,化简不等式,再利用
,去掉绝对值符号进行求解(2)先根据所给范围,化简不等式,再利用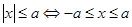 求解,利用最值求
求解,利用最值求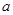 的范围.
的范围.规律总结:处理绝对值不等式问题,主要从去掉绝对值符号入手,往往讨论变量的范围去掉绝对值符号,变成分段函数求解问题;证明问题还往往涉及
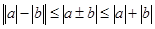 的应用.
的应用.试题解析:(1)解:原不等式可化为
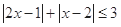 ,
,当
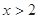 时,
时,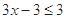 ,则
,则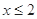 ,无解;
,无解; 当
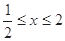 时,
时,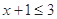 ,则
,则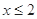 ,∴
,∴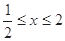 ;
; 当
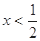 时,
时,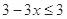 ,则
,则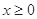 ,∴
,∴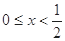 ,
, 综上所述:原不等式的解集为
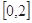 .
. (2)原不等式可化为
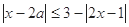 ,
,∵
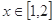 ,∴
,∴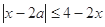 ,
, 即
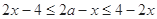 ,
,故
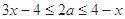 对
对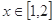 恒成立,
恒成立, 当
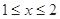 时,
时,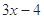 的最大值为
的最大值为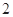 ,
,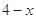 的最小值为
的最小值为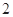 ,
,∴实数
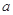 的集合为
的集合为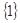 .
.
练习册系列答案
相关题目

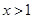 时,
时, 与
与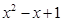
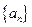 的前
的前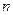 项和为
项和为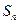 ,若
,若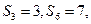 则
则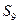 等于 。
等于 。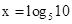 ,
,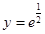 ,
,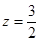 ,(e是自然对数的底数),则
,(e是自然对数的底数),则
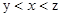


 ,
, ,则
,则 与
与 的大小关系为 .
的大小关系为 .