��Ŀ����
����Ŀ��ij��ѧ���ڸ�һ��ѧ�ڿ�����Ӿѡ�Σ�Ϊ���˽��һѧ��ϲ����Ӿ�Ƿ����Ա��йأ���ѧУ��100����һ�����������ʾ����飬�õ�������������
ϲ����Ӿ | ��ϲ����Ӿ | �ϼ� | |
���� | 10 | ||
�� | 20 | ||
�ϼ� |
��֪����100���������ȡ1�˳鵽ϲ����Ӿ��ѧ���ĸ���Ϊ![]() ��
��
��1���뽫��������������������
��2�����ж��Ƿ���99.9%�İ�����Ϊϲ����Ӿ���Ա��йأ���˵��������ɣ�
��3����֪�ڱ������ѧ������5�����Լװ࣬����3��ϲ����Ӿ���ִ���5��ѧ���������ȡ2�ˣ���ǡ����1��ϲ����Ӿ�ĸ��ʣ�
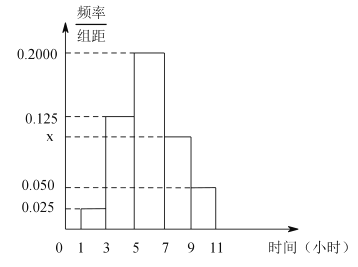
������ٽ�ֵ�������ο���
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ�� ������
������![]() ��
��
���𰸡���1������������������2����![]() �İ�����Ϊϲ����Ӿ���Ա��йأ���3��
�İ�����Ϊϲ����Ӿ���Ա��йأ���3��![]() .
.
��������
�����������1�������������![]() ����������2�����ݸ����Ĺ�ʽ
����������2�����ݸ����Ĺ�ʽ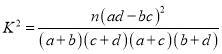 ������ϵ����ֵ���Ա��ٽ�ֵ������
������ϵ����ֵ���Ա��ٽ�ֵ������![]() ������
������![]() �İ�����Ϊϲ����Ӿ���Ա��йأ������أ���3��
�İ�����Ϊϲ����Ӿ���Ա��йأ������أ���3��![]() ��ѧ����ϲ����Ӿ��
��ѧ����ϲ����Ӿ��![]() ��ѧ����Ϊ
��ѧ����Ϊ![]() ������
������![]() ��ѧ����Ϊ
��ѧ����Ϊ![]() ����ȡ
����ȡ![]() ��ѧ�����г����п�������������ҳ�����
��ѧ�����г����п�������������ҳ�����![]() ��ѧ���������ȡ
��ѧ���������ȡ![]() �ˣ�ǡ����
�ˣ�ǡ����![]() ��ϲ����Ӿ����������ȼ�������ĸ���.
��ϲ����Ӿ����������ȼ�������ĸ���.
�����������1����Ϊ��100���������ȡ1�˳鵽ϲ����Ӿ��ѧ���ĸ���Ϊ![]() ��
��
����ϲ����Ӿ��ѧ������Ϊ![]() �ˣ�������������������������������������1��
�ˣ�������������������������������������1��
����Ů����20�ˣ���������40�ˣ��������������£�
ϲ����Ӿ | ��ϲ����Ӿ | �ϼ� | |
���� | 40 | 10 | 50 |
�� | 20 | 30 | 50 |
�ϼ� | 60 | 40 | 100 |
������������������������������������������������������������������������������������������������4��
��Ϊ![]() �������������������������������������� 7��
�������������������������������������� 7��
������99.9%�İ�����Ϊϲ����Ӿ���Ա��йأ�������������������������������������������8��
��2��5��ѧ����ϲ����Ӿ��3��ѧ����Ϊ![]() ������2��ѧ����Ϊ1��2����ȡ2��ѧ���������п������Ϊ
������2��ѧ����Ϊ1��2����ȡ2��ѧ���������п������Ϊ![]() ����10�֣�����������������10��
����10�֣�����������������10��
����ǡ��1��ϲ����Ӿ�Ŀ������Ϊ![]() ����6�֣��������������������� 11��
����6�֣��������������������� 11��
���ԣ�ǡ����1��ϲ����Ӿ�ĸ���Ϊ![]() ������������������������12��
������������������������12��

 ��У����ϵ�д�
��У����ϵ�д�