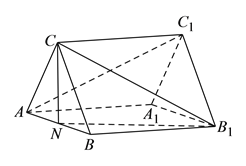
题目内容
【题目】已知两条不重合的直线![]() 和两个不重合的平面
和两个不重合的平面![]() ,若
,若![]() ,则下列四个命题:①若
,则下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ; ③若
; ③若![]() ,则
,则![]() ;④若
;④若![]() ,则
,则![]() ,其中正确命题的个数是( )
,其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
【答案】C
【解析】对于①,若![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() ,所以①正确;对于②,若
,所以①正确;对于②,若![]() 时,
时, ![]() ,不能推出
,不能推出![]() ,所以不能得出
,所以不能得出![]() ,②错误;对于③,若
,②错误;对于③,若![]() ,则
,则![]() ,而
,而![]() ,由面面垂直的判定定理有
,由面面垂直的判定定理有![]() ,所以③正确;对于④,若
,所以③正确;对于④,若![]() ,又
,又![]() ,
, ![]() ,则
,则![]() 的关系不能确定,可能平行,可能相交,可能异面,④错误.正确的有①③,故正确命题的个数为2.选C.
的关系不能确定,可能平行,可能相交,可能异面,④错误.正确的有①③,故正确命题的个数为2.选C.
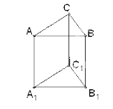
点睛:本题主要考查了立体几何中的线面位置关系,属于易错题.在①中考查了线面垂直的性质定理,线面垂直,则线线垂直;在②中,反例:见下图,直三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 面
面![]() ,但平面
,但平面![]() 平面
平面![]() ,故②是错误的; ③是考查面面垂直的判定定理;在④中, 直线
,故②是错误的; ③是考查面面垂直的判定定理;在④中, 直线![]() 的位置关系不能确定,可能平行,可能相交,可能异面.
的位置关系不能确定,可能平行,可能相交,可能异面.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);

(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() )
)