题目内容
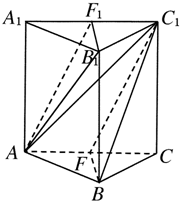
如图,三棱柱A1B1C1-ABC的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点.
(I)求证:B1C∥平面AC1M;
(II)求证:平面AC1M⊥平面AA1B1B.
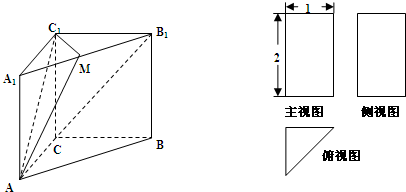
(I)求证:B1C∥平面AC1M;
(II)求证:平面AC1M⊥平面AA1B1B.

证明:(I)由三视图可知三棱柱A1B1C1-ABC为直三棱柱,底面是等腰直角三角形且∠ACB=90°,连接A1C,设A1C∩AC1=O.连接MO,由题意可知A1O=CO,A1M=B1M,所以MO∥B1C.
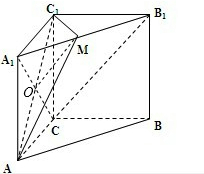 ∵MO?平面AC1M,B1C?平面AC1M
∵MO?平面AC1M,B1C?平面AC1M
∴B1C∥平面AC1M;
(II)∵A1C1=B1C1,点M是A1B1的中点
∴C1M⊥A1B1,
∵平面A1B1C1⊥平面AA1B1B,平面A1B1C1∩平面AA1B1B=A1B1,
∴C1M⊥平面AA1B1B
∵C1M?平面AC1M
∴平面AC1M⊥平面AA1B1B.
 ∵MO?平面AC1M,B1C?平面AC1M
∵MO?平面AC1M,B1C?平面AC1M∴B1C∥平面AC1M;
(II)∵A1C1=B1C1,点M是A1B1的中点
∴C1M⊥A1B1,
∵平面A1B1C1⊥平面AA1B1B,平面A1B1C1∩平面AA1B1B=A1B1,
∴C1M⊥平面AA1B1B
∵C1M?平面AC1M
∴平面AC1M⊥平面AA1B1B.

练习册系列答案
相关题目


 、
、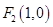 ,动点
,动点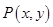 ,且满足
,且满足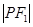 、
、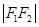 、
、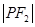
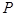 的轨迹
的轨迹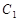 的方程;
的方程;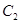 的方程为
的方程为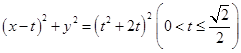 ,过点
,过点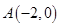 的直线
的直线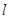 与曲线
与曲线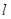 被曲线
被曲线 截得的线段长的最小值.
截得的线段长的最小值.