题目内容
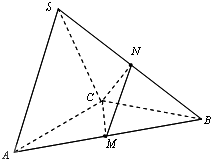
作等腰直角三角形ABC的斜边AB的中线CD，沿CD将△ABC折叠，使平面ACD⊥平面BCD，则折叠后AC与BC的夹角∠ACB的度数为______．
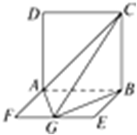
如图所示：
折叠后∠ACD=∠BCD=45°，AD⊥CD，BD⊥CD，则∠ADB为二面角A-CD-B的平面角，
又平面ACD⊥平面BCD，所以∠ADB=90°，所以△ADB为等腰直角三角形，
设AD=1，则AC=BC=AB=
，所以△ABC为正三角形，
所以∠ACB=60°．
故答案为：600．
折叠后∠ACD=∠BCD=45°，AD⊥CD，BD⊥CD，则∠ADB为二面角A-CD-B的平面角，
又平面ACD⊥平面BCD，所以∠ADB=90°，所以△ADB为等腰直角三角形，
设AD=1，则AC=BC=AB=
| 2 |
所以∠ACB=60°．
故答案为：600．
练习册系列答案
名校课堂系列答案
相关题目
