题目内容
已知定点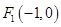 、
、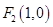 ,动点
,动点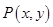 ,且满足
,且满足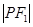 、
、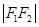 、
、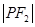
成等差数列.
(1)求点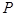 的轨迹
的轨迹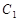 的方程;
的方程;
(2)若曲线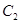 的方程为
的方程为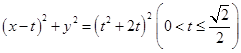 ,过点
,过点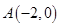 的直线
的直线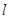 与曲线
与曲线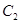 相切,
相切,
求直线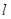 被曲线
被曲线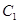 截得的线段长的最小值.
截得的线段长的最小值.
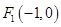 、
、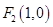 ,动点
,动点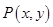 ,且满足
,且满足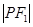 、
、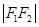 、
、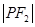
成等差数列.
(1)求点
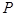 的轨迹
的轨迹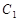 的方程;
的方程;(2)若曲线
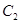 的方程为
的方程为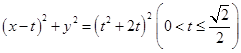 ,过点
,过点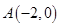 的直线
的直线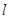 与曲线
与曲线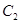 相切,
相切,求直线
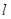 被曲线
被曲线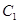 截得的线段长的最小值.
截得的线段长的最小值.(1) :(2)
:(2) .
.
 :(2)
:(2) .
.试题分析:(1)利用题中的条件得到椭圆的定义,求出椭圆的实轴长与焦距,然后利用
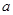 、
、 、
、 之间的关
之间的关系求出
 的值,从而确定点
的值,从而确定点 的轨迹
的轨迹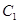 的方程;(2)先设直线
的方程;(2)先设直线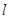 的方程为
的方程为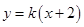 ,利用直线
,利用直线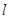 与圆
与圆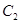
相切,结合
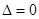 确定
确定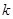 和
和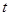 之间的等量关系,然后联立直线与椭圆
之间的等量关系,然后联立直线与椭圆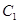 的方程,求出交点的坐标,利用两点
的方程,求出交点的坐标,利用两点间的距离公式求出弦长的表达式,利用换元法将弦长表达式进行化简,并利用函数单调性求出弦长的最小
值.
(1)由
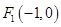 、
、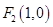 ,
, 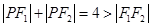 ,
,根据椭圆定义知
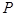 的轨迹为以
的轨迹为以 、
、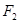 为焦点的椭圆,
为焦点的椭圆,其长轴
 ,焦距
,焦距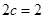 ,短半轴
,短半轴 ,故
,故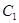 的方程为
的方程为 .
.(2)过点
 与
与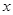 轴垂直的直线不与圆
轴垂直的直线不与圆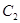 相切,故可设
相切,故可设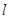 :
: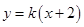 ,
,由直线
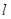 与曲线
与曲线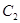 相切得
相切得 ,化简得
,化简得 ,
,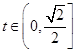 ,
,由
 ,解得
,解得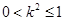 ,
,联立
 ,消去
,消去 整理得
整理得 ,
,直线
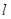 被曲线
被曲线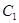 截得的线段一端点为
截得的线段一端点为 ,设另一端点为
,设另一端点为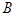 ,
,解方程可得
 ,
,有
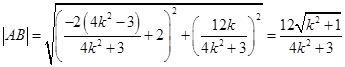 ,
,令
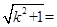 ,则
,则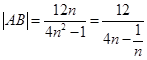 ,
,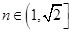 ,
,考查函数
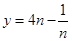 的性质知
的性质知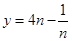 在区间
在区间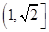 上是增函数,
上是增函数,所以
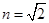 时,
时,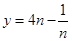 取最大值
取最大值 ,从而
,从而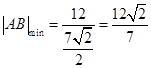 .
.
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
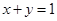 ,则
,则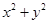 的最小值为 .
的最小值为 .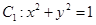 与圆
与圆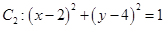 ,过动点
,过动点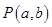 分别作圆
分别作圆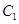 、圆
、圆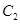 的切线
的切线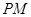 、
、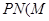 、
、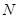 分别为切点),若
分别为切点),若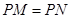 ,则
,则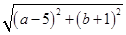 的最小值是 .
的最小值是 .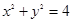 ,直线
,直线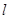 :
: 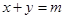 ,若圆O上恰有3个点到
,若圆O上恰有3个点到
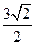 ,则实数a为( ).
,则实数a为( ).