题目内容
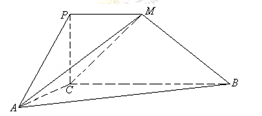
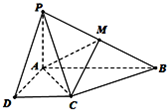
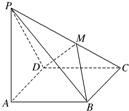
如图,在圆锥PO中,已知PO=
,⊙O的直径AB=2,C是
的中点,D为AC的中点.
(Ⅰ)证明:平面POD⊥平面PAC;
(Ⅱ)求二面角B-PA-C的余弦值.

| 2 |
 |
| AB |
(Ⅰ)证明:平面POD⊥平面PAC;
(Ⅱ)求二面角B-PA-C的余弦值.

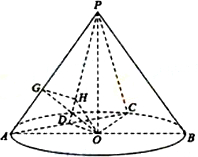
(Ⅰ)连接OC,
∵OA=OC,D是AC的中点
∴AC⊥OD
又∵PO⊥底面⊙O,AC?底面⊙O
∴AC⊥PO
∵OD、PO是平面POD内的两条相交直线
∴AC⊥平面POD,
而AC?平面PAC
∴平面POD⊥平面PAC
(Ⅱ)在平面POD中,过O作OH⊥PD于H,由(Ⅰ)知,平面POD⊥平面PAC
所以OH⊥平面PAC,
又∵PA?平面PAC
∴PA⊥HO
在平面PAO中,过O作OG⊥PA于G,连接GH,则有PA⊥平面OGH,从而PA⊥HG.故∠OGH为二面角B-PA-C的平面角
在Rt△ODA中,OD=OA•sin45°=
在Rt△ODP中,OH=
=
=
在Rt△OPA中,OG=
=
=
在Rt△OGH中,sin∠OGH=
=
=
所以cos∠OGH=
=
=
故二面角B-PA-C的余弦值为
∵OA=OC,D是AC的中点
∴AC⊥OD
又∵PO⊥底面⊙O,AC?底面⊙O
∴AC⊥PO
∵OD、PO是平面POD内的两条相交直线
∴AC⊥平面POD,
而AC?平面PAC
∴平面POD⊥平面PAC
(Ⅱ)在平面POD中,过O作OH⊥PD于H,由(Ⅰ)知,平面POD⊥平面PAC
所以OH⊥平面PAC,
又∵PA?平面PAC
∴PA⊥HO
在平面PAO中,过O作OG⊥PA于G,连接GH,则有PA⊥平面OGH,从而PA⊥HG.故∠OGH为二面角B-PA-C的平面角
在Rt△ODA中,OD=OA•sin45°=
| ||
| 2 |
在Rt△ODP中,OH=
| PO•OD | ||
|
| ||||||
|
| ||
| 5 |
在Rt△OPA中,OG=
| PO•OA | ||
|
| ||
|
| ||
| 3 |
在Rt△OGH中,sin∠OGH=
| OH |
| OG |
| ||||
|
| ||
| 5 |
所以cos∠OGH=
| 1-sin2∠OGH |
1-
|
| ||
| 5 |
故二面角B-PA-C的余弦值为
| ||
| 5 |


练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目