题目内容
19．函数f（x）=lnx-$\frac{1}{2}$x2的单调增区间为（ ）| A． | （-∞，-1）和（0，1） | B． | （0，1） | C． | （-1，0）和（1，+∞） | D． | （1，+∞） |
分析 求出函数的导数，利用导函数大于0，即可求得f（x）的单调增区间．
解答 解：∵f（x）=lnx-$\frac{1}{2}$x2的定义域为（0，+∞），
f′（x）=$\frac{1}{x}-x$，∴由f′（x）＞0得：$\frac{1}{x}-x$＞0，解得0＜x＜1，
∴函数f（x）=lnx-$\frac{1}{2}$x2的单调增区间为为（0，1）．
故选：B．
点评 本题考查利用导数研究函数的单调性，注重标根法的考查与应用，属于基础题．
练习册系列答案
相关题目
9．已知全集U=R，A={x|x＜1}，B={y|-|x|+y=2}，则集合∁U（A∪B）=（ ）
| A． | {x|1≤x＜2} | B． | {x|1＜x≤2} | C． | {x|x≥1} | D． | {x|x≤2} |
10．若复数Z满足$\overline Z$（1+i）=2i，则在复平面内Z对应的点的坐标是（ ）
| A． | （1，1） | B． | （1，-l） | C． | （-l，1） | D． | （-l，-l） |
4．
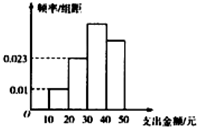为了解学生在课外活动方面的支出情况，抽取了n个同学进行调查，结果显示这些学生的支出金额（单位：元）都在[10，50]，其中支出金额在[30，50]的学生有134人，频率分布直方图如图所示，则n=（ ）
为了解学生在课外活动方面的支出情况，抽取了n个同学进行调查，结果显示这些学生的支出金额（单位：元）都在[10，50]，其中支出金额在[30，50]的学生有134人，频率分布直方图如图所示，则n=（ ）| A． | 150 | B． | 160 | C． | 180 | D． | 200 |
8．函数f（x）=sin（x+$\frac{π}{2}$）图象的一个对称中心为（ ）
| A． | （$\frac{π}{2}$，0） | B． | （0，1） | C． | （0，0） | D． | （-$\frac{π}{4}$，0） |