题目内容
16.已知函数 f(x)=ax+(1-a)lnx+$\frac{1}{x}$(a∈R)(I)当a=0时,求 f(x)的极值;
(Ⅱ)当a<0时,求 f(x)的单调区间;
(Ⅲ)方程 f(x)=0的根的个数能否达到3,若能请求出此时a的范围,若不能,请说明理由.
分析 (Ⅰ)代入a的值,求出定义域,求导,利用导数求出单调区间,即可求出极值.
(Ⅱ)直接对f(x)求导,根据a的不同取值,讨论f(x)的单调区间.
(Ⅲ)由第二问的结论,即函数的单调区间来讨论f(x)的零点个数.
解答 解:(Ⅰ)f(x)其定义域为(0,+∞).…(1分)
当a=0时,f(x)=$lnx+\frac{1}{x}$,f'(x)=$\frac{1}{x}-\frac{1}{{x}^{2}}=\frac{x-1}{{x}^{2}}$.
令f'(x)=0,解得x=1,
当0<x<1时,f'(x)<0;当x>1时,f'(x)>0.
所以f(x)的单调递减区间是(0,1),单调递增区间是(1,+∞);
所以x=1时,f(x)有极小值为f(1)=1,无极大值 …(3分)
(Ⅱ) f'(x)=a-$\frac{a-1}{x}-\frac{1}{{x}^{2}}=\frac{a{x}^{2}-(a-1)x-1}{{x}^{2}}=\frac{(ax+1)(x-1)}{{x}^{2}}$ (x>0)…(4分)
令f'(x)=0,得x=1或x=-$\frac{1}{a}$
当-1<a<0时,1<-$\frac{1}{a}$,令f'(x)<0,得0<x<1或x>-$\frac{1}{a}$,
令f'(x)>0,得1<x<-$\frac{1}{a}$;
当a=-1时,f'(x)=-$\frac{(x-1)^{2}}{x}≤0$.
当a<-1时,0<-$\frac{1}{a}$<1,令f'(x)<0,得0<x<-$\frac{1}{a}$或x>1,
令f'(x)>0,得-$\frac{1}{a}$<a<1;
综上所述:
当-1<a<0时,f(x)的单调递减区间是(0,1),(-$\frac{1}{a},+∞$),
单调递增区间是(1,-$\frac{1}{a}$);
当a=-1时,f(x)的单调递减区间是(0,+∞);
当a<-1时,f(x)的单调递减区间是(0,-$\frac{1}{a}$),(1,+∞),单调递增区间是$(-\frac{1}{a},1)$
…(10分)
(Ⅲ)a≥0∴$f'(x)=\frac{(ax+1)(x-1)}{{x}^{2}}(x>0)$
f'(x)=0(x>0)仅有1解,方程f(x)=0至多有两个不同的解.
(注:也可用fmin(x)=f(1)=a+1>0说明.)
由(Ⅱ)知-1<a<0时,极小值 f(1)a+1>0,方程f(x)=0至多在区间(-$\frac{1}{a},+∞$)上有1个解.
a=-1时f(x)单调,方程f(x)=0至多有1个解.;
a<-1时,$f(-\frac{1}{a})<f(1)=a+1<0$,方程
f(x)=0仅在区间内(0,-$\frac{1}{a}$)有1个解;
故方程f(x)=0的根的个数不能达到3.…(14分)
点评 本题主要考查利用导数求函数极值和单调区间的方法,考查考生化归思想的应用能力,属于中档题.

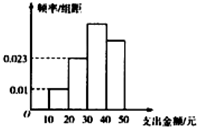 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
| A. | ($\frac{π}{2}$,0) | B. | (0,1) | C. | (0,0) | D. | (-$\frac{π}{4}$,0) |
| A. | 126 | B. | 26 | C. | 13 | D. | 12 |