题目内容
12.已知点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)上,F1,F2是这条双曲线上的两个焦点,$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0,且△F1PF2的三条边的长度成等差数列,则此双曲线的离心率的值为5.分析 设|PF2|,|PF1|,|F1F2|成等差数列,且分别设为m-d,m,m+d,则由双曲线定义和勾股定理求出m=4d=8a,c=$\frac{5}{2}$d,由此求得离心率的值.
解答 解:设|PF2|,|PF1|,|F1F2|成等差数列,且分别设为m-d,m,m+d,
则由双曲线定义和勾股定理可知:m-(m-d)=2a,m+d=2c,(m-d)2+m2=(m+d)2,
解得m=4d=8a,c=$\frac{5}{2}$d,故离心率e=$\frac{c}{a}$=5,
故答案为:5.
点评 本题主要考查等差数列的定义和性质,以及双曲线的简单性质的应用,属于中档题.

练习册系列答案
相关题目
3.若复数$\frac{a+i}{2i}$的实部和虚部相等,则实数a等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
20.已知I为全集,且B∩(∁IA)=B.求A∩B=( )
| A. | A | B. | B | C. | ∁IB | D. | ∅ |
17.已知cos(θ+π)=-$\frac{1}{3}$,则sin(2θ+$\frac{π}{2}$)=( )
| A. | $\frac{7}{9}$ | B. | $-\frac{7}{9}$ | C. | $\frac{{4\sqrt{2}}}{9}$ | D. | $-\frac{{4\sqrt{2}}}{9}$ |
4.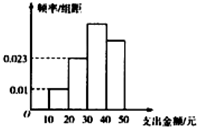 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
2.在△ABC中,若$cosA=\frac{sinB}{sinC}$,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 钝角三角形 |